Question
A motor powers a model car so that after starting from rest, the car travels s inches in t seconds, where s = 16t  . Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
. Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
- 4

- 16


- 16t
The correct answer is: 16
speed = 
Distance =  .
.
Time = t
Speed = 

Related Questions to study
Two different points on a number line are both 3 units from the point with coordinate −4. The solution to which of the following equations gives the coordinates of both points?
Two different points on a number line are both 3 units from the point with coordinate −4. The solution to which of the following equations gives the coordinates of both points?
In the xy-plane, the graph of 2x2 − 6x + 2y2 + 2y = 45 is a circle. What is the radius of the circle?
In the xy-plane, the graph of 2x2 − 6x + 2y2 + 2y = 45 is a circle. What is the radius of the circle?
A gear ratio r: s is the ratio of the number of teeth of two connected gears. The ratio of the number of revolutions per minute (rpm) of two gear wheels is s: r. In the diagram below, Gear A is turned by a motor. The turning of Gear A causes Gears B and C to turn as well.
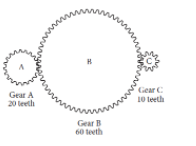
If Gear A is rotated by the motor at a rate of 100 rpm, what is the number of revolutions per minute for Gear C?
A gear ratio r: s is the ratio of the number of teeth of two connected gears. The ratio of the number of revolutions per minute (rpm) of two gear wheels is s: r. In the diagram below, Gear A is turned by a motor. The turning of Gear A causes Gears B and C to turn as well.

If Gear A is rotated by the motor at a rate of 100 rpm, what is the number of revolutions per minute for Gear C?
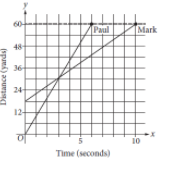
The graph above shows the positions of Paul and Mark during a race. Paul and Mark each ran at a constant rate, and Mark was given a head start to shorten the distance he needed to run. Paul finished the race in 6 seconds, and Mark finished the race in 10 seconds. According to the graph, Mark was given a head start of how many yards?
The graph of a y-intercept is the point at which the graph intersects the y-axis. We know that any point on the y-axis has an x-coordinate of 0. As a result, the x-coordinate of a y-intercept is 0.
The steps for determining the y-intercept of a function y = f (x),
• We simply replace x = 0 in it.
• Determine y.
• as the point, represent the y-intercept (0, y).
Here are some y-intercept examples.
• The y-intercept of y = 5x² + 2 is (0, 2) because we get y = 5(0)² + 2 = 2 when we substitute x = 0.
• The y-intercept of y = -5ex is (0, -5) because we get y = -5e0 = -5 when we substitute x = 0.

The graph above shows the positions of Paul and Mark during a race. Paul and Mark each ran at a constant rate, and Mark was given a head start to shorten the distance he needed to run. Paul finished the race in 6 seconds, and Mark finished the race in 10 seconds. According to the graph, Mark was given a head start of how many yards?
The graph of a y-intercept is the point at which the graph intersects the y-axis. We know that any point on the y-axis has an x-coordinate of 0. As a result, the x-coordinate of a y-intercept is 0.
The steps for determining the y-intercept of a function y = f (x),
• We simply replace x = 0 in it.
• Determine y.
• as the point, represent the y-intercept (0, y).
Here are some y-intercept examples.
• The y-intercept of y = 5x² + 2 is (0, 2) because we get y = 5(0)² + 2 = 2 when we substitute x = 0.
• The y-intercept of y = -5ex is (0, -5) because we get y = -5e0 = -5 when we substitute x = 0.
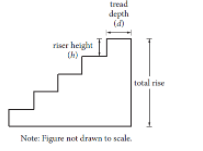
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway.
The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)
An architect can apply the riser-tread formula '2h + d = 25', where h is the height of the riser and d is the depth of tread in inches while creating a stairway. The riser heights and tread depths for every step in a staircase are the same for that staircase.
A stairway's riser count equals the number of steps it has. For instance, the stairs have five steps. A staircase's overall rise equals the sum of its riser heights.

When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway.
The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)
An architect can apply the riser-tread formula '2h + d = 25', where h is the height of the riser and d is the depth of tread in inches while creating a stairway. The riser heights and tread depths for every step in a staircase are the same for that staircase.
A stairway's riser count equals the number of steps it has. For instance, the stairs have five steps. A staircase's overall rise equals the sum of its riser heights.
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
|
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
|
The growth rate of the sunflower from day 14 to day 35 is nearly constant. On this interval, which of the following equations best models the height h, in centimeters, of the sunflower t days after it begins to grow?
The growth rate of the sunflower from day 14 to day 35 is nearly constant. On this interval, which of the following equations best models the height h, in centimeters, of the sunflower t days after it begins to grow?
Between 1497 and 1500, Amerigo Vespucci embarked on two voyages to the New World. According to Vespucci’s letters, the first voyage lasted 43 days longer than the second voyage, and the two voyages combined lasted a total of 1,003 days. How many days did the second voyage last?
Between 1497 and 1500, Amerigo Vespucci embarked on two voyages to the New World. According to Vespucci’s letters, the first voyage lasted 43 days longer than the second voyage, and the two voyages combined lasted a total of 1,003 days. How many days did the second voyage last?
Which expression is equivalent to (2x2 − 4) − (−3x2 + 2x − 7) ?
Which expression is equivalent to (2x2 − 4) − (−3x2 + 2x − 7) ?
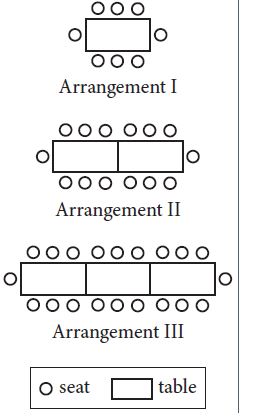
A project coordinator at a banquet hall is given the task of arranging seating for an awards ceremony. The figure above shows the first three possible arrangements of tables and the maximum number of seats in each arrangement. If the number of seats in each successive arrangement is increased by 6 over the preceding arrangement, which of the following represents the maximum number of seats around n tables?

A project coordinator at a banquet hall is given the task of arranging seating for an awards ceremony. The figure above shows the first three possible arrangements of tables and the maximum number of seats in each arrangement. If the number of seats in each successive arrangement is increased by 6 over the preceding arrangement, which of the following represents the maximum number of seats around n tables?
If  , what is 2x in the terms of a?
, what is 2x in the terms of a?
If  , what is 2x in the terms of a?
, what is 2x in the terms of a?
During a storm, the atmospheric pressure in a certain location fell at a constant rate of 3.4 millibars (mb) per hour over a 24-hour time period. Which of the following is closest to the total drop in atmospheric pressure, in millimeters of mercury (mm Hg), over the course of 5 hours during the 24-hour time period? (Note: 1,013 mb = 760 mm Hg)
During a storm, the atmospheric pressure in a certain location fell at a constant rate of 3.4 millibars (mb) per hour over a 24-hour time period. Which of the following is closest to the total drop in atmospheric pressure, in millimeters of mercury (mm Hg), over the course of 5 hours during the 24-hour time period? (Note: 1,013 mb = 760 mm Hg)
Ryan has 1,500 yards of yarn. He wants to knit at least 2 scarves and at least 3 hats. Each scarf requires 300 yards of yarn, and each hat requires 120 yards of yarn. If s represents the number of scarves and h represents the number of hats, which of the following systems of inequalities represents this situation?
A collection of more than one inequality in one or more variables is known as a system of inequalities. Systems of inequalities are helpful when a problem's potential solutions are subject to several constraints, and a variety of potential solutions are required.
¶An infinite number of ordered pair solutions for inequality in the set, each specified by a region in a rectangular coordinate plane. When two inequalities are considered, the collection of simultaneously ordered pair solutions is defined by the intersection of these sets.
¶Systems of inequalities can be solved slightly differently than systems of linear equations because the substitution and elimination methods are not applied. Only the limitations of the inequality signs, ≤, and ≥, are responsible for this.
Ryan has 1,500 yards of yarn. He wants to knit at least 2 scarves and at least 3 hats. Each scarf requires 300 yards of yarn, and each hat requires 120 yards of yarn. If s represents the number of scarves and h represents the number of hats, which of the following systems of inequalities represents this situation?
A collection of more than one inequality in one or more variables is known as a system of inequalities. Systems of inequalities are helpful when a problem's potential solutions are subject to several constraints, and a variety of potential solutions are required.
¶An infinite number of ordered pair solutions for inequality in the set, each specified by a region in a rectangular coordinate plane. When two inequalities are considered, the collection of simultaneously ordered pair solutions is defined by the intersection of these sets.
¶Systems of inequalities can be solved slightly differently than systems of linear equations because the substitution and elimination methods are not applied. Only the limitations of the inequality signs, ≤, and ≥, are responsible for this.
Which of the following is closest to the equation of the line of best fit shown?
Which of the following is closest to the equation of the line of best fit shown?
Nutritional Information for 1-Ounce Servings of Seeds and Nuts
|
Seed or nut |
Calories |
Total fat (grams) |
Protein (grams) |
|
Pecan |
198 |
20.2 |
3.0 |
|
Pistachio |
80 |
6.5 |
3.0 |
|
Pumpkin |
159 |
13.9 |
8.5 |
|
Sunflower |
166 |
14.6 |
5.9 |
|
Walnut |
185 |
18.5 |
4.3 |
(1 pound = 16 ounces)
Nutritional Information for 1-Ounce Servings of Seeds and Nuts
|
Seed or nut |
Calories |
Total fat (grams) |
Protein (grams) |
|
Pecan |
198 |
20.2 |
3.0 |
|
Pistachio |
80 |
6.5 |
3.0 |
|
Pumpkin |
159 |
13.9 |
8.5 |
|
Sunflower |
166 |
14.6 |
5.9 |
|
Walnut |
185 |
18.5 |
4.3 |
(1 pound = 16 ounces)





