Maths-
SAT
Easy
Question
Recommended Daily Intake of Potassium
|
Age |
Potassium (mg) |
| 0-6 months |
400 |
| 7-11 months |
700 |
| 1-3 years |
3,000 |
| 4-8 years |
3,800 |
| 9-13 years |
4,500 |
| 14-17 years |
4,700 |
| 18 years and up |
4,700 |
Andrea's recommended daily intake of potassium is 50% greater than that of her two-year-old brother. What is the least possible age, in years, of Andrea?
The correct answer is: 9
Her brother is 2 years. So, the intake will be 3000
50% greater than 3000 = 1.5 × 3000 = 4500 & it is for 9 – 13 years
Least possible age can be 9 years
Related Questions to study
Maths-

Note: Figure not drawn to scale.
In the figure above, ABC and DEC are right triangles. If CD = 20 and the tangent of angle ABC is 2.5, what is the length of segment ED ?

Note: Figure not drawn to scale.
In the figure above, ABC and DEC are right triangles. If CD = 20 and the tangent of angle ABC is 2.5, what is the length of segment ED ?
Maths-SAT
Maths-
Lines t and w are parallel in the xy-plane. The equation of line t is 4x + 7 y = 14, and line w passes through (-3, 8). What is the value of they-intercept of line w?
Lines t and w are parallel in the xy-plane. The equation of line t is 4x + 7 y = 14, and line w passes through (-3, 8). What is the value of they-intercept of line w?
Maths-SAT
Maths-
The numbers of people, in millions, who visited Amusement Park A and Amusement Park B in 2009 through 2013 are listed in the table below. What is the positive difference between the mean number of people, in millions, who visited Amusement Park B · and the mean number of people, in millions, who visited Amusement Park A during those years? (Round your answer to the nearest tenth.)
|
Location |
2009 |
2010 |
2011 |
2012 |
2013 |
| Amusement Park A |
15.7 |
15.2 |
14.4 |
14.1 |
12.3 |
| Amusement Park B |
15.9 |
16.0 |
16.1 |
16.0 |
16.2 |
The numbers of people, in millions, who visited Amusement Park A and Amusement Park B in 2009 through 2013 are listed in the table below. What is the positive difference between the mean number of people, in millions, who visited Amusement Park B · and the mean number of people, in millions, who visited Amusement Park A during those years? (Round your answer to the nearest tenth.)
|
Location |
2009 |
2010 |
2011 |
2012 |
2013 |
| Amusement Park A |
15.7 |
15.2 |
14.4 |
14.1 |
12.3 |
| Amusement Park B |
15.9 |
16.0 |
16.1 |
16.0 |
16.2 |
Maths-SAT
Maths-
p = 9n - (2n + k)
The profit p, in dollars, from producing and selling n units of a certain product is given by the equation above, where k is a constant. If200 units are produced and sold for a profit of $1275, what is the value of k?
p = 9n - (2n + k)
The profit p, in dollars, from producing and selling n units of a certain product is given by the equation above, where k is a constant. If200 units are produced and sold for a profit of $1275, what is the value of k?
Maths-SAT
Maths-
The function f has the property that, for all x , 3f(x) = f(3x). If f(6) = 12, what is the value of f(2)?
The function f has the property that, for all x , 3f(x) = f(3x). If f(6) = 12, what is the value of f(2)?
Maths-SAT
Maths-
Radioactive substances decay over time. The mass M, in grams, of a particular radioactive substance d days after the beginning of an experiment is shown in the table below.
|
Number of days, d |
Mass, M (grams) |
|
0 |
120.00 |
|
30 |
103.21 |
|
60 |
88.78 |
|
90 |
76.36 |
Radioactive substances decay over time. The mass M, in grams, of a particular radioactive substance d days after the beginning of an experiment is shown in the table below.
|
Number of days, d |
Mass, M (grams) |
|
0 |
120.00 |
|
30 |
103.21 |
|
60 |
88.78 |
|
90 |
76.36 |
Maths-SAT
Maths-
The table below shows the number of lakes in the United Kingdom classified by alkalinity and depth.
|
Depth class |
Alkalinity Class |
|||
|
Low |
Medium |
High |
Total |
|
| Shallow |
87 |
61 |
209 |
357 |
| Moderate |
227 |
86 |
110 |
423 |
| Deep |
130 |
35 |
21 |
186 |
| Total |
444 |
182 |
340 |
966 |
The table below shows the number of lakes in the United Kingdom classified by alkalinity and depth.
|
Depth class |
Alkalinity Class |
|||
|
Low |
Medium |
High |
Total |
|
| Shallow |
87 |
61 |
209 |
357 |
| Moderate |
227 |
86 |
110 |
423 |
| Deep |
130 |
35 |
21 |
186 |
| Total |
444 |
182 |
340 |
966 |
Maths-SAT
Maths-
a(-3x-1) + x = 7x - 2
The equation above has no solutions, and a is a constant. What is the value of a ?
a(-3x-1) + x = 7x - 2
The equation above has no solutions, and a is a constant. What is the value of a ?
Maths-SAT
Maths-
A signal from a spacecraft orbiting Mercury travels to Earth at a speed of 3 x 108 meters per second. If the distance between Earth and the spacecraft is 2.0221 x 108 kilometers, which of the following ·is closest to the number of minutes it will take for a signal from the spacecraft to reach Earth?
(1 kilometer= 1,000 meters)
A signal from a spacecraft orbiting Mercury travels to Earth at a speed of 3 x 108 meters per second. If the distance between Earth and the spacecraft is 2.0221 x 108 kilometers, which of the following ·is closest to the number of minutes it will take for a signal from the spacecraft to reach Earth?
(1 kilometer= 1,000 meters)
Maths-SAT
Maths-
y = (x-h)2 (x+h)(x+k)
The equation above is graphed in the xy-plane. If h and k are positive constants and h  k, how many distinct x-intercepts does the graph have?
k, how many distinct x-intercepts does the graph have?
y = (x-h)2 (x+h)(x+k)
The equation above is graphed in the xy-plane. If h and k are positive constants and h  k, how many distinct x-intercepts does the graph have?
k, how many distinct x-intercepts does the graph have?
Maths-SAT
Maths-

The scatterplot above represents the salary y, in thousands of dollars, and the number of years of experience, x, for each of six employees at a company. A line of best fit for the data is also shown. Which of the following could be an equation of the line of best fit?

The scatterplot above represents the salary y, in thousands of dollars, and the number of years of experience, x, for each of six employees at a company. A line of best fit for the data is also shown. Which of the following could be an equation of the line of best fit?
Maths-SAT
Maths-
x(x + 1) + 2(x + 1) = ax2 +bx+ c
In the equation above, a, b, and c are constants. If the equation is true for all values of x, what is the value of a + b + c ?
x(x + 1) + 2(x + 1) = ax2 +bx+ c
In the equation above, a, b, and c are constants. If the equation is true for all values of x, what is the value of a + b + c ?
Maths-SAT
Maths-
kx+ y = 1
y = -x2 + k
In the system of equations above, k is a constant. When the equations are graphed in the xy-plane, the graphs intersect at exactly two points. Which of the following CANNOT be the value of k ?
kx+ y = 1
y = -x2 + k
In the system of equations above, k is a constant. When the equations are graphed in the xy-plane, the graphs intersect at exactly two points. Which of the following CANNOT be the value of k ?
Maths-SAT
Maths-
A physician prescribes a treatment in which a patient takes 2 teaspoons of a medication every 6 hours for 5 days. According to the prescription, how many teaspoons of the medication should the patient take in a 24-hour period?
A physician prescribes a treatment in which a patient takes 2 teaspoons of a medication every 6 hours for 5 days. According to the prescription, how many teaspoons of the medication should the patient take in a 24-hour period?
Maths-SAT
Maths-
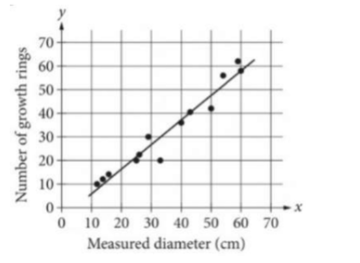
For a sample of 13 red alder trees, an arborist measured each tree’s diameter, in centimeters (cm), at a height of 1.4 meters. The arborist then counted the number of growth rings at this height. Each point in the scatterplot represents the diameter and number of rings for each tree. A line of best fit for these data is also shown.
A red alder tree will be selected at random from the sample. What is the probability that the selected tree will have a measured diameter that is greater that is greater than 30 cm?

For a sample of 13 red alder trees, an arborist measured each tree’s diameter, in centimeters (cm), at a height of 1.4 meters. The arborist then counted the number of growth rings at this height. Each point in the scatterplot represents the diameter and number of rings for each tree. A line of best fit for these data is also shown.
A red alder tree will be selected at random from the sample. What is the probability that the selected tree will have a measured diameter that is greater that is greater than 30 cm?
Maths-SAT





