To remove the drawbacks of Rutherford’s nuclear atomic model and explain the origin of the production of the spectrum of Hydrogen and Hydrogen-like species (such as Li2+, He+, etc.). In 1913, Neil Bohr put forward an atomic model based on Planck’s quantum radiation theory.
Quantum mechanics serves as the foundation for the contemporary model of an atom.
Let’s have a look at Bohr’s atomic model.
Bohr’s Model of the Atom
Two developments played a major role in formulating the Bohr model of the atom. These were:
- The dual personality of electromagnetic radiation means that radiations possess particle-like and wave-like properties.
- Experimental results of atomic spectra can explain only by assuming quantised electronic energy levels in atoms.
Bohr retains the essential features of the Rutherford model of the atom. However, to account for the stability of the atom, he introduced the concept of the stationary orbit.
Bohr’s Atomic model explains that a small positively charged nucleus is surrounded by negatively charged electrons revolving in fixed orbits. Bohr concluded that an electron would have more energy if it is far from the nucleus. In contrast, it will have less energy if situated near the nucleus.
Postulates of Bohr’s Atomic Model
1. An atom comprises three particles, i.e., neutrons, protons, and electrons.
–Electrons possess a negative charge, neutrons have no charge, whereas protons have a positive charge. They are neutral. The atom, on the whole, is electrically neutral due to an equal number of negative electrons and positive protons.
-The neutrons and protons are located in a small nucleus at the centre of the atom. Due to the existence of protons, the nucleus is positively charged. This nucleus is responsible for almost the entire mass of the atom.
2. The electron in an atom behaves as a material particle. It revolves throughout the nucleus in a fixed concentric circular path called orbit or shell.
-As the electron in these orbits is associated with a certain amount of energy, these circular paths are also called energy levels or energy shells.
3. As the distance between the energy level and nucleus increases, the energy associated with a certain energy level increases. Therefore, E1 < E2 < E3 … .
4. These energy levels are represented by K, L, M, N, etc., starting from the nucleus. The values of the principal quantum number, n, for these levels are:
- 1st energy level, i.e., n = 1, is represented as K-shell, and it can hold up to 2 electrons.
- 2nd energy level, i.e., n = 2, is represented as an L-shell and can hold up to 8 electrons.
- 3rd energy level, i.e., n = 3, is represented as an M-shell and can contain up to 18 electrons.
- 4th energy level, i.e., n = 4, is represented as an N-shell and can contain a maximum of 32 electrons.
The orbits can increase in the same way.
5. As long as an electron revolves in a particular orbit, it can neither absorbs nor emits energy. That is why these orbits are also called stationary orbits.
6. When an electron jumps from a lower energy level n1 with the energy E1 to a higher level n2 with energy E2, the electron absorbs energy in photons. When an electron bounces from a higher energy level n2 with the energy E2 to a lower level n1 with energy E1, the electron absorbs energy in the form of photons.
7. According to the quantum theory, the energy absorbed or radiated is equal to
E,sub>1 – E1 = ΔE = h𝜈,
where 𝜈 = frequency of the radiation absorbed or released by the electron and
h = Planck’s constant.
This equation is known as Bohr’s frequency condition. The released energy appears as a spectral line in the emission spectrum.
8. The permitted orbits are those for which the angular momentum of an electron is an integral multiple of h/ 2𝜋, where h = Planck’s constant.
If 𝘷 is the velocity and m is the mass of the electron in an authorised orbit of radius r, then,
L = m𝘷r = n (h/ 2𝜋)
where n = an integral (called principal quantum number), which denotes the number of the orbit in which the electron is revolving and equals 1, 2, 3, etc. This equation is known as the Bohr quantisation postulate or principle of quantisation of angular momentum.
Achievements of the Bohr Model
Following are the achievements of Bohr’s atomic model.
- According to the Bohr model, the electron does not lose energy as long as it revolves in a particular orbit. Therefore, gradual loss of energy of the electron is not possible. Hence, the atom is stable.
- When an element is heated, its electrons absorb energy and jump from a lower orbit to a higher one. At the higher level, they are unstable and hence jump back to the lower level. In this process, energy is released and gives the emission spectrum. Thus, the Bohr model explains very well the origin of the production of the emission spectrum.
- When electromagnetic radiation is passed through the solution of a substance, some of its wavelengths are absorbed by the substance. These absorbed wavelengths cause the excitation of its electron. Hence, the missing photons appear as dark lines in the spectrum. Therefore, Bohr’s atomic model also explains the absorption spectrum’s origin.
- A bluish glow is obtained when an electric discharge is passed through a discharge tube filled with Hydrogen gas at very low pressure. By analysing this glow with the prism, different spectral lines are obtained in the IR, UV, and visible regions. The group of these spectral lines is called the emission spectrum of Hydrogen.
This spectrum consists of many lines, which are grouped into five series, i.e., Lyman series, Balmer series, Paschen series, Brackett series, and Pfund series, and is called spectral series.
Limitations of Bohr’s Atomic Model
- The Bohr model explains the spectrum of species having only one electron, i.e., H, He+, Li2+, Be3+, etc. Simply put, it does not explain the spectra of atoms having more than one electron.
- It does not explain why an excited electron shows an emission spectrum when put in a magnetic field (Zeeman effect) or an electric field (Stark effect).
- de Broglie suggested that an electron has a dual character, i.e., an electron, like light, behaves both as a wave and as a material particle. But, the Bohr model assumed that an electron behaves as a material particle.
- According to Bohr, circular orbits, in which the electrons revolve, are planar. But modern research has shown that an electron moves around the nucleus in three-dimensional space, i.e., in all three (x, y, z) axes.
- Bohr assumed that the electron revolves around the nucleus in circular orbits at a definite distance from the nucleus, and their moving velocity is also fixed. But, it is against Heisenberg’s uncertainty principle.
- Bohr’s theory predicts the origin of only one spectral line from an electron between two given energy states. But under a spectroscope of the strong resolution, its single line is found to split into several very closely related lines. Bohr’s model could not explain the multiple fine structures of spectral lines.
- There is no explanation for the assumption that the electron can rotate only in those orbits in which the angular momentum of the electron, i.e., m𝘷r, is a whole number multiple of h/ 2𝜋, i.e., why not h/ 3𝜋, h/ 4𝜋, etc.
Summary
Neil Bohr overcame Rutherford’s model’s difficulties in his Hydrogen atom model. He hypothesised that electrons move around the nucleus in circular orbits.
Only certain orbits can exist, and each orbit corresponds to a specific energy. He calculated the energy of electrons in various orbits and predicted the distance between the electron and neutron for each orbit.
Despite many achievements, his model failed to explain the spectra of multi-electron atoms and the wave character of an electron.
Frequently Asked Questions
Q1. What are the facts that favour the Bohr model?
Answer: Some facts favour the Bohr model of the atom:
- The experimental values of radii and energies of the permissible orbits in the Hydrogen atom are good and agree with those calculated based on the Bohr model.
- Bohr’s concept of the static state of electrons explains Hydrogen’s ejection and absorption spectra and other only one-electron atoms.
- The experimental value of the frequencies of the spectral lines of the Hydrogen spectrum is in close agreement with the frequencies of the same lines calculated with the help of Bohr’s theory.
- The experimental value of the Rydberg constant for Hydrogen, RH, is in close agreement with that calculated from Bohr’s theory.
Q2. What are the advantages of the Bohr model of the atom?
Answer: Bohr’s atomic model satisfactorily explains the spectra of species having one electron, i.e., H, Li2+, He+, etc.
Moreover, Bohr’s postulates can also be used for calculating:
- Radii of various orbits in Hydrogen and other only one electron species.
- The velocity of an electron with which it revolves in orbits of Hydrogen and other only one electron species.
- The electron’s energy moves in orbits around the nucleus in Hydrogen and other only one electron species.
Q3. What is Bohr’s radius?
Answer: The radius of the first orbit (n = 1) of H-atom (Z = 1) or Hydrogen like species is represented by r0 and called Bohr’s radius.
The value of (r1)H = 0.529 Å = 0.529 x 10-10 m.

Relevant Articles
Butanoic Acid – Structure, Properties, Uses
Butanoic Acid The carboxylic acid, butanoic acid, has the structural …
Butanoic Acid – Structure, Properties, Uses Read More »
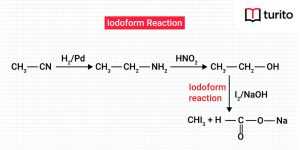
Read More >>What is Iodoform? Characteristics and Uses
Iodoform The formula for Iodoform is CHI3. It is biotic …
What is Iodoform? Characteristics and Uses Read More »
Read More >>Lattice Energy – Explanation, Factors & Formulas
Lattice Energy Lattice energy evaluates the intensity of the ionic …
Lattice Energy – Explanation, Factors & Formulas Read More »
Read More >>Lead Acetate – Definition, Properties, Uses
Lead Acetate Have you ever licked lipstick when you sketch …
Lead Acetate – Definition, Properties, Uses Read More »
Read More >>


















Comments: