Chemistry-
General
Easy
Question
In the given reaction sequence,

the final product [BJ will be:
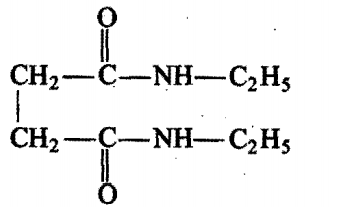
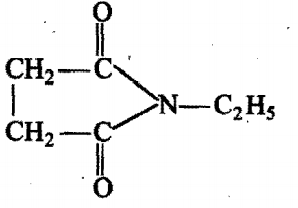
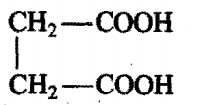
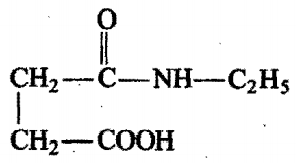
The correct answer is: 
Related Questions to study
Chemistry-
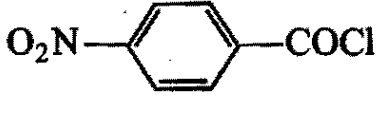
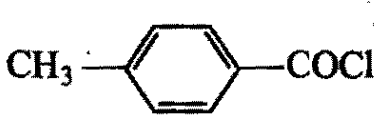
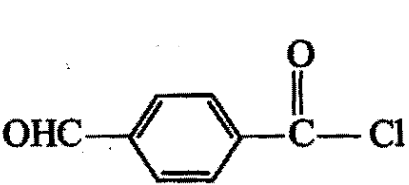
Arrange the following compounds in the decreasing order of reactivity for hydrolysis reaction:
1) 
2) 
3) 
4) 
Arrange the following compounds in the decreasing order of reactivity for hydrolysis reaction:
1) 
2) 
3) 
4) 
Chemistry-General
Chemistry-
 The product obtained in above reaction will be :
The product obtained in above reaction will be :
 The product obtained in above reaction will be :
The product obtained in above reaction will be :
Chemistry-General
Chemistry-
The percentage of nitrogen in urea is:
The percentage of nitrogen in urea is:
Chemistry-General
Maths-
In a packet of 40 pens, 12 are red. So, what % age are red pens?
In a packet of 40 pens, 12 are red. So, what % age are red pens?
Maths-General
Chemistry-
Consider the following compounds, which of these will release CO2 with 5% NaHCO3 ?
i) 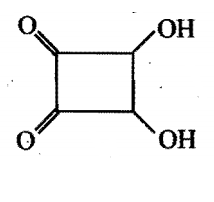
ii) 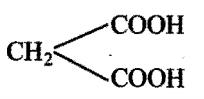
iii) 
Consider the following compounds, which of these will release CO2 with 5% NaHCO3 ?
i) 
ii) 
iii) 
Chemistry-General
Chemistry-
Identify the product' Y' in the following reaction sequence:

Identify the product' Y' in the following reaction sequence:

Chemistry-General
Chemistry-
In homogeneous catalytic reactions, there are three alternative paths A,B and C (shown in the figure) which one of the following indicates the relative ease with which the reaction can take place?

In homogeneous catalytic reactions, there are three alternative paths A,B and C (shown in the figure) which one of the following indicates the relative ease with which the reaction can take place?

Chemistry-General
Chemistry-
In a spontaneous adsorption process
In a spontaneous adsorption process
Chemistry-General
Chemistry-
Graph between log  and log P is a straight line at angle 0 45 with intercept OA as shown Hence ,
and log P is a straight line at angle 0 45 with intercept OA as shown Hence , at a pressure of 2 atm is
at a pressure of 2 atm is

Graph between log  and log P is a straight line at angle 0 45 with intercept OA as shown Hence ,
and log P is a straight line at angle 0 45 with intercept OA as shown Hence , at a pressure of 2 atm is
at a pressure of 2 atm is

Chemistry-General
Maths-
If  and
and  then
then
If  and
and  then
then
Maths-General
Maths-
Assertion : For  the volume of the parallel piped formed by vectors
the volume of the parallel piped formed by vectors  and
and  is maximum (The vectors form a right-handed system)
is maximum (The vectors form a right-handed system)
Reason: The volume of the parallel piped having three coterminous edges  and
and 
For such questions, we should know the formula of a parallelepiped. We should also know how to take a scalar product.
Assertion : For  the volume of the parallel piped formed by vectors
the volume of the parallel piped formed by vectors  and
and  is maximum (The vectors form a right-handed system)
is maximum (The vectors form a right-handed system)
Reason: The volume of the parallel piped having three coterminous edges  and
and 
Maths-General
For such questions, we should know the formula of a parallelepiped. We should also know how to take a scalar product.
Maths-
Assertion (A): Let  . If
. If  such that
such that  is collinear with
is collinear with  and
and  is perpendicular to
is perpendicular to  is possible, then
is possible, then  .
.
Reason (R): If  and
and  are non-zero, non-collinear vectors, then
are non-zero, non-collinear vectors, then  can be expressed as
can be expressed as  where
where  is collinear with
is collinear with  and
and  is perpendicular to
is perpendicular to 
Assertion (A): Let  . If
. If  such that
such that  is collinear with
is collinear with  and
and  is perpendicular to
is perpendicular to  is possible, then
is possible, then  .
.
Reason (R): If  and
and  are non-zero, non-collinear vectors, then
are non-zero, non-collinear vectors, then  can be expressed as
can be expressed as  where
where  is collinear with
is collinear with  and
and  is perpendicular to
is perpendicular to 
Maths-General
Maths-
Statement  If
If  are distinct non-negative numbers and the vectors â
are distinct non-negative numbers and the vectors â  and
and  are coplanar then
are coplanar then  is arithmetic mean of
is arithmetic mean of  and
and  .
.
Statement -2: Parallel vectors have proportional direction ratios.
Statement  If
If  are distinct non-negative numbers and the vectors â
are distinct non-negative numbers and the vectors â  and
and  are coplanar then
are coplanar then  is arithmetic mean of
is arithmetic mean of  and
and  .
.
Statement -2: Parallel vectors have proportional direction ratios.
Maths-General
Maths-
If  and
and  is a vector satisfying
is a vector satisfying  .
.
Assertion  can be expressed in terms of
can be expressed in terms of  and
and  .
.
Reason 
If  and
and  is a vector satisfying
is a vector satisfying  .
.
Assertion  can be expressed in terms of
can be expressed in terms of  and
and  .
.
Reason 
Maths-General
Maths-
If  are non-zero vectors such that
are non-zero vectors such that  then
then
Assertion  : Least value of
: Least value of  is
is 
Reason (R): The expression  is least when magnitude of
is least when magnitude of  is
is 
If  are non-zero vectors such that
are non-zero vectors such that  then
then
Assertion  : Least value of
: Least value of  is
is 
Reason (R): The expression  is least when magnitude of
is least when magnitude of  is
is 
Maths-General



