Question
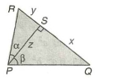
If l, m, n are the  terms of a G.P which are +ve, then
terms of a G.P which are +ve, then 
- 3
- 2
- 1
- 0

The formula for the nth term of the geometric progression is:
an = arn-1
where, a is the first term
- r is the common ratio
- n is the number of the term which we want to find.
The correct answer is: 0
Given : l, m, n are the  terms of a G.P
terms of a G.P
We know that in GP

where,
- a is the first term
- r is the common ratio
- n is the number of the term which we want to find.
Using this :

Substituting these values in :

We know that

Using these formulas and further simplifying


Thus,  0
0
Related Questions to study
The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm

The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm

Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.
Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.