Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

If the normal at the points P_i (x_i, y_i), i = 1 to 4 on the hyperbola xy = c² are concurrent at the point Q(h, k), then $fraction numerator open parentheses x subscript 1 end subscript plus x subscript 2 end subscript plus x subscript 3 end subscript plus x subscript 4 end subscript close parentheses open parentheses y subscript 1 end subscript plus y subscript 2 end subscript plus y subscript 3 end subscript plus y subscript 4 end subscript close parentheses over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction$ is equal to

$\frac{h k}{c^{4}}$
$\frac{h^{2} k^{2}}{c^{6}}$
$\frac{\sqrt{| h k |}}{c^{3}}$
$\frac{h k}{c^{4}}$

The correct answer is: $fraction numerator h k over denominator c to the power of 4 end exponent end fraction$

Equation of normal at any point P(ct, $blank fraction numerator c over denominator t end fraction$ ) on xy = c², is xt³ yt ct⁴ + c = 0
If it passes through Q (h, k), then
ct⁴ ht³ + kt c = 0
If its roots are t₁, t₂, t₃ and t₄, then
t₁ + t₂ + t₃ + t₄ = $h over c$
ct₁ + ct₂ + ct₃ + ct₄ = h
x_i = h, t₁ t₂ t₃ = $blank fraction numerator k over denominator c end fraction$ , t₁ t₂ t₃ t₄ =1 (ct₁)(ct₂)(ct₃)(ct₄)= c⁴
 $fraction numerator c over denominator t subscript i end subscript end fraction equals k$ y_i = k and x₁x₂ x₃ x₄
= c⁴ $fraction numerator sum x subscript i end subscript capital sigma y subscript i end subscript over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction equals negative fraction numerator h k over denominator c to the power of 4 end exponent end fraction$

Related Questions to study

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

According to Huckel’s rule a compound is said to be aromatic if it contains

According to Huckel’s rule a compound is said to be aromatic if it contains

Chemistry-General

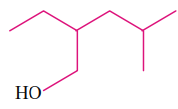structure is

structure is

Chemistry-General

parallel

Two volatile liquids A and B differ in their boiling points by 0 15 C The process which can be used to separate them is

Two volatile liquids A and B differ in their boiling points by 0 15 C The process which can be used to separate them is

Chemistry-General

Consider the ellipse whose equation is $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ For certain pair of diameters of the above ellipse, the product of their slopes is equal to $negative fraction numerator b to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction$
The equations of two diameters are $y equals x$ and $3 y equals negative 2 x$ satisfying the condition mentioned above. Then the eccentricity of the ellipse is

Consider the ellipse whose equation is $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ For certain pair of diameters of the above ellipse, the product of their slopes is equal to $negative fraction numerator b to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction$
The equations of two diameters are $y equals x$ and $3 y equals negative 2 x$ satisfying the condition mentioned above. Then the eccentricity of the ellipse is

The smallest possible value of S $equals a subscript 1 end subscript times a subscript 2 end subscript times a subscript 3 end subscript plus b subscript 1 end subscript times b subscript 2 end subscript times b subscript 3 end subscript plus c subscript 1 end subscript times c subscript 2 end subscript times c subscript 3 end subscript text end text$ where $text end text a subscript 1 end subscript comma a subscript 2 end subscript comma a subscript 3 end subscript comma b subscript 1 end subscript comma b subscript 2 end subscript comma b subscript 3 end subscript comma c subscript 1 end subscript comma c subscript 2 end subscript comma c subscript 3 end subscript$ is a permutation of the number 1, 2, 3, 4, 5, 6, 7, 8, and 9 is

The smallest possible value of S $equals a subscript 1 end subscript times a subscript 2 end subscript times a subscript 3 end subscript plus b subscript 1 end subscript times b subscript 2 end subscript times b subscript 3 end subscript plus c subscript 1 end subscript times c subscript 2 end subscript times c subscript 3 end subscript text end text$ where $text end text a subscript 1 end subscript comma a subscript 2 end subscript comma a subscript 3 end subscript comma b subscript 1 end subscript comma b subscript 2 end subscript comma b subscript 3 end subscript comma c subscript 1 end subscript comma c subscript 2 end subscript comma c subscript 3 end subscript$ is a permutation of the number 1, 2, 3, 4, 5, 6, 7, 8, and 9 is

parallel

Statement 1 : The second degree equation $4 x to the power of 2 end exponent plus 9 y to the power of 2 end exponent minus 24 x plus 36 y minus 72 equals 0$ represents an ellipse Because
Statement 2 : $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 g x plus 2 f y plus c equals 0$ represents an ellipse if $capital delta equals a b c plus 2 f g h minus a f to the power of 2 end exponent minus b g to the power of 2 end exponent minus c h to the power of 2 end exponent not equal to 0$ and $h to the power of 2 end exponent greater than a b$

Statement 1 : The second degree equation $4 x to the power of 2 end exponent plus 9 y to the power of 2 end exponent minus 24 x plus 36 y minus 72 equals 0$ represents an ellipse Because
Statement 2 : $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 g x plus 2 f y plus c equals 0$ represents an ellipse if $capital delta equals a b c plus 2 f g h minus a f to the power of 2 end exponent minus b g to the power of 2 end exponent minus c h to the power of 2 end exponent not equal to 0$ and $h to the power of 2 end exponent greater than a b$

Statement-1: P is any point such that the chord of contact of tangents from P to the ellipse $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ touches $x to the power of 2 end exponent plus 4 y to the power of 2 end exponent equals 4$ The the tangents from P of $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ are at right angles and
Statement-2: The tangent from any point on the director circle of an ellipse are at right angles

Statement-1: P is any point such that the chord of contact of tangents from P to the ellipse $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ touches $x to the power of 2 end exponent plus 4 y to the power of 2 end exponent equals 4$ The the tangents from P of $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ are at right angles and
Statement-2: The tangent from any point on the director circle of an ellipse are at right angles

Statement-1: The distance of the tangent through (0, (d) from a focus of the ellipse $fraction numerator x to the power of 2 end exponent over denominator 16 end fraction plus fraction numerator y to the power of 2 end exponent over denominator 7 end fraction equals 1$ is 5
and
Statement-2: The locus of the foot of the perpendicular from a focus on any tangent to $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ is $x to the power of 2 end exponent plus y to the power of 2 end exponent equals a to the power of 2 end exponent$

Statement-1: The distance of the tangent through (0, (d) from a focus of the ellipse $fraction numerator x to the power of 2 end exponent over denominator 16 end fraction plus fraction numerator y to the power of 2 end exponent over denominator 7 end fraction equals 1$ is 5
and
Statement-2: The locus of the foot of the perpendicular from a focus on any tangent to $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ is $x to the power of 2 end exponent plus y to the power of 2 end exponent equals a to the power of 2 end exponent$

parallel

There are ‘n’ numbered seats around a round table. Total number of ways in which n n1 1 () < n persons can sit around the round table is equal to

There are ‘n’ numbered seats around a round table. Total number of ways in which n n1 1 () < n persons can sit around the round table is equal to

The IUPAC name of is

The IUPAC name of is

Chemistry-General

If the normal at any given point P on the ellipse $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ meets its
auxiliary circle at Q and R such that QOR = 90, where O is the centre
of ellipse, then

If the normal at any given point P on the ellipse $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ meets its
auxiliary circle at Q and R such that QOR = 90, where O is the centre
of ellipse, then

parallel

8-digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do not occupy odd places is

8-digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do not occupy odd places is

Given an in equation $open vertical bar 1 plus fraction numerator 2 over denominator x end fraction close vertical bar greater than 3$ whose solution set is given by $left parenthesis a comma 0 right parenthesis union left parenthesis 0 comma b right parenthesis$ then answer the following questions If solution set for $left parenthesis x plus 1 right parenthesis to the power of 2 end exponent less than left parenthesis 7 x minus 3 right parenthesis blank$ is (c,d), then a+b+c+d=

Given an in equation $open vertical bar 1 plus fraction numerator 2 over denominator x end fraction close vertical bar greater than 3$ whose solution set is given by $left parenthesis a comma 0 right parenthesis union left parenthesis 0 comma b right parenthesis$ then answer the following questions If solution set for $left parenthesis x plus 1 right parenthesis to the power of 2 end exponent less than left parenthesis 7 x minus 3 right parenthesis blank$ is (c,d), then a+b+c+d=

IUPAC name of ethers is

IUPAC name of ethers is

Chemistry-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.