Question
If the sides of a triangle are in the ratio 
then greatest angle is
- 900
- 1200
- 600
Hint:
The law of cosines generalizes the Pythagorean formula to all triangles. It says that c2, the square of one side of the triangle, is equal to a2 + b2, the sum of the squares of the the other two sides, minus 2ab cos C, twice their product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
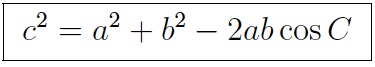
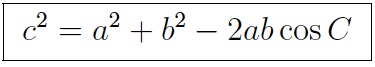
The correct answer is: 1200
If the sides of a triangle are in the ratio then greatest angle is
Angle c is greatest in triangle.
then greatest angle isAngle c is greatest in triangle.
Related Questions to study
A straight rod of length L has one of its ends at the origin and the other end at x=L If the mass per unit length of rod is given by Ax where A is constant where is its center of mass.
A straight rod of length L has one of its ends at the origin and the other end at x=L If the mass per unit length of rod is given by Ax where A is constant where is its center of mass.
In 
then 
s denotes the semi-perimeter of the triangle ABC, ∆ its area and R the radius of the circle circumscribing the triangle ABC i.e., R is the circum-radius.
In then
s denotes the semi-perimeter of the triangle ABC, ∆ its area and R the radius of the circle circumscribing the triangle ABC i.e., R is the circum-radius.
A small disc of radius 2 cm is cut from a disc of radius 6 cm. If the distance between their centrer is 3.2 cm, what is the shift in the center of mass of the disc...
A small disc of radius 2 cm is cut from a disc of radius 6 cm. If the distance between their centrer is 3.2 cm, what is the shift in the center of mass of the disc...
Let be the moment of inertia of a uniform square plate about an axis AB that passes through its center and is parallel to two of its sides CD is a line in the plane of the plate that passes through the center of the plate and makes an angle of Q with AB. The moment of inertia of the plate about the axis CD is then equal to....
Let be the moment of inertia of a uniform square plate about an axis AB that passes through its center and is parallel to two of its sides CD is a line in the plane of the plate that passes through the center of the plate and makes an angle of Q with AB. The moment of inertia of the plate about the axis CD is then equal to....
If 
is positive, then 
lies between
If is positive, then lies between
If 
then the Δk is
If then the Δk is
If 
then 
=
If then =
If 
and 
, 
then 
If and , then
In a 
If 
then 
In a If then
Assertion (A): If 
then 
Reason (R): If 
then 
Assertion (A): If then
Reason (R): If then
Concentrations of the atmospheric 
have been rising becaue of
Concentrations of the atmospheric have been rising becaue of
Two disc of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio 1:3. The moment of inertia of these disc about the respective axes passing through their center and perpendicular to their planes will be in the ratio
Two disc of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio 1:3. The moment of inertia of these disc about the respective axes passing through their center and perpendicular to their planes will be in the ratio
of 
(alum) can be replaced by
of (alum) can be replaced by
If the sides of triangles are 8,15,17 then radius of the Circumcenter is
In this question, we have to find the radius of the circumcenter. The given sides of triangle is triad of the Pythagoras theorem then the triangle is right angled.
If the sides of triangles are 8,15,17 then radius of the Circumcenter is
In this question, we have to find the radius of the circumcenter. The given sides of triangle is triad of the Pythagoras theorem then the triangle is right angled.
is bent in to a circular loop with center at O as shown in figure. The moment of inertia of the loop about the axis xx’ is ....
