Question
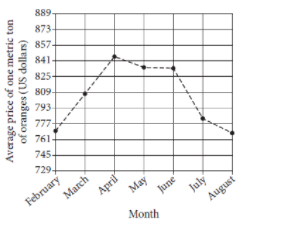
The line graph above shows the average price of one metric ton of oranges, in dollars, for each of seven months in 2014.
Between which two consecutive months shown did the average price of one metric ton of oranges decrease the most?
- March to April
- May to June
- June to July
- July to August
The correct answer is: June to July
STEP BY STEP SOLUTION
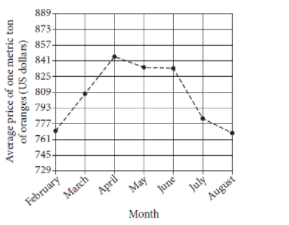
By observing the line graph the average price of one metric ton of oranges decreases most from June to July.
Related Questions to study
Use polynomial identities to factor the polynomials or simplify the expressions : 
Polynomial identities are equations that are true for all possible values of the variable. We can perform polynomial multiplication by applying the distributive property to the multiplication of polynomials.
Use polynomial identities to factor the polynomials or simplify the expressions : 
Polynomial identities are equations that are true for all possible values of the variable. We can perform polynomial multiplication by applying the distributive property to the multiplication of polynomials.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle (using the fourth row).
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle (using the fourth row).
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The expansion of (x + y)n can be also found using the Pascal’s triangle using the (n+1)th row of the triangle.
Use the binomial theorem to expand the expressions: 
The expansion of (x + y)n can be also found using the Pascal’s triangle using the (n+1)th row of the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n, we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n, we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
A Medium sized Shipping box with side length s units has a volume of S3 cubic units.
a. A Large shipping box has side lengths that are 3 units longer than the medium shipping box. Write a binomial expression for the volume of the large shipping box .
b. Expand the polynomial in part A to simplify the volume of the large shipping box ?
The volume of a cuboid with side length a is, V = a3.
A Medium sized Shipping box with side length s units has a volume of S3 cubic units.
a. A Large shipping box has side lengths that are 3 units longer than the medium shipping box. Write a binomial expression for the volume of the large shipping box .
b. Expand the polynomial in part A to simplify the volume of the large shipping box ?
The volume of a cuboid with side length a is, V = a3.
The dimensions of a rectangle are shown. Write the area of the rectangle as a sum of cubes .

The area of a rectangle with length l and width w is A = lw
The dimensions of a rectangle are shown. Write the area of the rectangle as a sum of cubes .

The area of a rectangle with length l and width w is A = lw





