Physics-
General
Easy
Question
Consider a disc rotating in the horizontal plane with a constant angular speed 
about its centre 
. The disc has a shaded region on one side of the diameter and an unshanded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles 
and 
are simultaneously projected at an angle towards 
. The velocity of projection is in the 
plane and is same for both pebbles with respect to the disc. Assume that i) they land back on the disc before the disc has completed 
rotation. ii) their range is less than half the disc radius, and (iii) remains constant throughout. Then
- lands in the shaded region and in the unshaded region
- lands in the unshaded region and in the shaded region
- Both and land in the unshaded region
- Both and land in the shaded region
lands in the shaded region and in the unshaded region
lands in the unshaded region and in the shaded region
and land in the unshaded region
and land in the shaded region
The correct answer is: lands in the shaded region and in the unshaded region
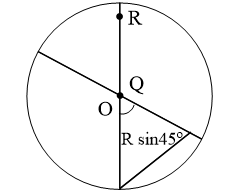
To reach the unshaded portion particle needs to travel horizontal range greater than 
or 
but its range is less than 
. So it will fall on shaded portion
is near to origin, its velocity will be nearly along 
so its will fall in unshaded portion
Related Questions to study
physics-
From an inclined plane two particles are projected with same speed at same angle 
, one up and other down the plane as shown in figure. Which of the following statements 
is/are correct?
From an inclined plane two particles are projected with same speed at same angle , one up and other down the plane as shown in figure. Which of the following statements is/are correct?
physics-General
maths-
If 
then 
is
If then is
maths-General
chemistry-
The free energy change for the following reactions aregivenbelow-C2H2(g)+
O2(g)→2CO2(g)+H2O(l);DG°=–1234KJC(s)+O2(g)→CO2(g);DG°=–394KJ H2(g)+
O2(g)→H2O(l);DG°=–237KJWhatisthestandardfreeenergychangeforthe reactionH2(g)+2C(s)→C2H2(g)-
The free energy change for the following reactions aregivenbelow-C2H2(g)+O2(g)→2CO2(g)+H2O(l);DG°=–1234KJC(s)+O2(g)→CO2(g);DG°=–394KJ H2(g)+O2(g)→H2O(l);DG°=–237KJWhatisthestandardfreeenergychangeforthe reactionH2(g)+2C(s)→C2H2(g)-
chemistry-General
chemistry-
The value of DH–DE for the following reaction at 27°C will be,2NH3(g)→N2(g)+3H2(g)
The value of DH–DE for the following reaction at 27°C will be,2NH3(g)→N2(g)+3H2(g)
chemistry-General
chemistry-
If at 298K the bond energies of C–H,C–C,C=C and H–H bonds are respectively 414,347,615and 435KJmol–1,thevalueofenthalpy change for there action H2C=CH2(g)+H2(g)→CH3–CH3(g)at298 K will be-
If at 298K the bond energies of C–H,C–C,C=C and H–H bonds are respectively 414,347,615and 435KJmol–1,thevalueofenthalpy change for there action H2C=CH2(g)+H2(g)→CH3–CH3(g)at298 K will be-
chemistry-General
maths-
If 
then n=
If then n=
maths-General
maths-
There were two women participating in a chess tournament Every participant played two games with the other participants the number of games that the men played between themselves proved to exceed by 66 the number of games that the men played with the women The number of participants is
There were two women participating in a chess tournament Every participant played two games with the other participants the number of games that the men played between themselves proved to exceed by 66 the number of games that the men played with the women The number of participants is
maths-General
maths-
153 games were played at a chess tournament with each contestant playing once against each of the others The number of participants is
153 games were played at a chess tournament with each contestant playing once against each of the others The number of participants is
maths-General
maths-
The number of different ways in which a committee of 4 members formed out of 6 Asians, 3 Europeans and 4 Americans if the committee is to have at least one from each of the 3 regional groups is
The number of different ways in which a committee of 4 members formed out of 6 Asians, 3 Europeans and 4 Americans if the committee is to have at least one from each of the 3 regional groups is
maths-General
maths-
A committee of5 is to be formed from 6 boys and 5 girls The number of ways that the committee can be formed so that the committee contains at least one boy and one girl having majority of boys is
A committee of5 is to be formed from 6 boys and 5 girls The number of ways that the committee can be formed so that the committee contains at least one boy and one girl having majority of boys is
maths-General
maths-
If n and are integers such that 
then n c (n‐l, r‐l)=
If n and are integers such that then n c (n‐l, r‐l)=
maths-General
maths-
maths-General
maths-
The least value of the natural number 
n satisfying 
The least value of the natural number n satisfying
maths-General
maths-
then (n, r)=
then (n, r)=
maths-General
maths-
then ‘n’ is
then ‘n’ is
maths-General
