Question
Some gaseous equilbrium are following -

then find out the relation between equilbrium constant -
The correct answer is: 
Related Questions to study
If some He gas is introduced into the equilibrium  at constant pressure and temperature then equilibrium constant of reaction
at constant pressure and temperature then equilibrium constant of reaction
If some He gas is introduced into the equilibrium  at constant pressure and temperature then equilibrium constant of reaction
at constant pressure and temperature then equilibrium constant of reaction
Normality of  solution nearly -
solution nearly -
Normality of  solution nearly -
solution nearly -
Grasses & many crop plants which possess hydathodes & exhibit guttation are
Grasses & many crop plants which possess hydathodes & exhibit guttation are
Path of energy flow in a n ecosystem is
Path of energy flow in a n ecosystem is
The principle functional group of the following compound is ................

The principle functional group of the following compound is ................

What will be the IUPAC name of the given compound ?

What will be the IUPAC name of the given compound ?

IUPAC name of the following compound will be ............

IUPAC name of the following compound will be ............

The correct IUPAC name of the compound
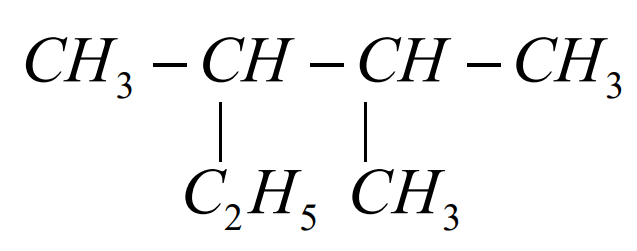
is....
The correct IUPAC name of the compound
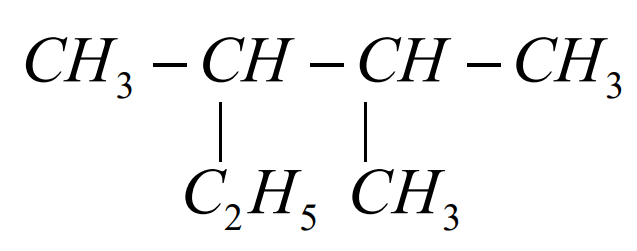
is....
Predict the IUPAC name of

Predict the IUPAC name of

What is the IUPAC name of the following compound?

What is the IUPAC name of the following compound?

Which IUPAC name correctly represents the following organic molecule ?

Which IUPAC name correctly represents the following organic molecule ?

The best arrangement of an energy system consisting of hawks, snakes, mice and grasses is
The best arrangement of an energy system consisting of hawks, snakes, mice and grasses is
The maximum and minimum values of  are
are
In this question, you have to find the maximum and minimum value of the function. Firstly find the local minimum and local maximum value put for that , put the value of 1st derivative in 2nd derivative to find local maximum and minimum value. If the 2nd derivative is positive then it is minimum else maximum. Put the same value to the main equation and find the minimum and maximum value.
The maximum and minimum values of  are
are
In this question, you have to find the maximum and minimum value of the function. Firstly find the local minimum and local maximum value put for that , put the value of 1st derivative in 2nd derivative to find local maximum and minimum value. If the 2nd derivative is positive then it is minimum else maximum. Put the same value to the main equation and find the minimum and maximum value.





