Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?

The combustion of glucose releases energy. The ratio of grams of glucose combusted to kilocalories of energy released is 12.0 to 45.0. How many grams of glucose must be combusted to provide 85.5 kilocalories of energy?

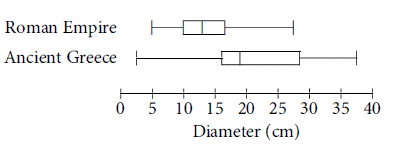
The Metropolitan Museum of Art has plates on display from the Roman Empire and ancient Greece. The box plots shown summarize the distributions of the diameters, in centimeters, of all the museum's plates from each region. How does the median diameter of the plates from the Roman Empire, r, compare to the median diameter of the plates from ancient Greece, g ?

$1 half x plus 5 equals k x plus 7$
In the given equation, k is a constant. The equation has no solution. What is the value of k ?

4x + y = 7
2x - 7y = 1
If (x, y) is the solution to the given system of equations, what is the value of x ?

x²-2x -1 = 0
The equation above has solutions $x equals n plus square root of k$ , and $x equals n minus square root of k$ , where n and k are positive integers. What is the value of n + k ?

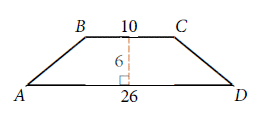
In the figure shown, $stack B C with bar on top$ is parallel to $stack A D with bar on top$ and AB = CD. What is the perimeter of quadrilateral ABCD?

4T - 8D = 12H
The given equation can be rewritten as T = aD + bH, where a and bare constants. What is the value of a ?

Two beach balls are each in the shape of a sphere. The larger beach ball has a diameter of 3x, and the smaller beach ball has a diameter of x. What is the ratio of the volume of the larger beach ball to the volume of the smaller beach ball?

y = (x - 1)(x + 2)(x + 2)
The graph in the xy-plane of the equation above contains the point (a, b). If -1 $less or equal than$ a $less or equal than$ 1, which of the following is NOT a possible value of b ?

Every term in a linear equation has an exponent of 1, so when it is graphed, it always results in a straight line. So, it is referred to as a "linear equation."
¶Both one-variable and two-variable linear equations exist. The linear equation formula is used to express a linear equation. There are numerous ways to accomplish this. For example, the linear equation can be expressed in standard, slope-intercept, or point-slope forms. Taking a linear equation in standard form,
¶Several methods for resolving linear equations in two variables include the graphical approach, substitution techniques, cross-multiplication techniques, elimination techniques, and determinant approaches.

y = (x - 1)(x + 2)(x + 2)
The graph in the xy-plane of the equation above contains the point (a, b). If -1 $less or equal than$ a $less or equal than$ 1, which of the following is NOT a possible value of b ?

Which expression is equivalent to (2x²+ 3x - 2) - (5x²- x - 7) ?

The equation h = 150 + 10t gives the total number of housing units, h, in a community t months after a new zoning law was passed. How many housing units are added to the community each month after the zoning law was passed?

A graph illustrates the connection between two or more variables. An upward-sloping curve denotes a clear correlation between the two variables, and a curve with a downward slope denotes a negative correlation between the two variables.
A relationship between two variables can be measured and described using the statistical approach of correlation. Typically, the two variables are not changed. Therefore, two identical-person scores are necessary for the association. These results are represented as X and Y.

The equation h = 150 + 10t gives the total number of housing units, h, in a community t months after a new zoning law was passed. How many housing units are added to the community each month after the zoning law was passed?

x² -10x + y² + 6y = 2
The graph in the xy-plane of the equation above is a circle. What are the coordinates of the center of the circle?

If x > 0, which of the following is equivalent to $1 over x plus fraction numerator 1 over denominator 2 x end fraction ?$

From 1990 to 2001, German currency included coins called pfennigs, worth 1 pfennig each, and groschen, worth 10 pfennigs each. Which equation represents the number of pfennig coins, p, and groschen coins, g, that have a combined value of 85 pfennigs?

Isolating a variable entails rearranging an algebraic equation so that one variable stands alone. A goal is to select a set of operations that will leave the variable of interest on one side of the equal sign while putting all other terms on the other.
¶To isolate a quantity in a formula or equation:
1. Make a note of the original equation. If necessary, convert the word problem or context into an equation.
2. Begin isolating the desired quantity by performing the operation on both sides of the equation.
3. Repeat Step 2 until you have isolated the desired quantity.

From 1990 to 2001, German currency included coins called pfennigs, worth 1 pfennig each, and groschen, worth 10 pfennigs each. Which equation represents the number of pfennig coins, p, and groschen coins, g, that have a combined value of 85 pfennigs?