Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

If x_n > x_n–1>...> x₂ > x₁ > 1 then the value of $log subscript straight x subscript 1 end subscript invisible function application log subscript straight x subscript 2 end subscript invisible function application log subscript straight x subscript 3 end subscript invisible function application horizontal ellipsis log subscript straight x subscript straight n end subscript invisible function application x subscript n$ $blank to the power of x subscript n minus 1 end subscript superscript up right diagonal ellipsis to the power of x subscript 1 end exponent end superscript end exponent$ is equal to-

0
1
2
None of these

The correct answer is: 0

$log subscript x subscript 1 end subscript end subscript invisible function application blank$ $log subscript x subscript 3 end subscript end subscript invisible function application blank$ ... $log subscript x subscript n minus 1 end subscript end subscript invisible function application blank$ $open parentheses x subscript n minus 1 end subscript to the power of x subscript n minus 2 end subscript superscript. to the power of. to the power of. x subscript 1 end subscript end exponent end exponent end superscript end exponent log subscript x subscript n end subscript end subscript invisible function application x subscript n end subscript close parentheses$
= $log subscript x subscript 1 end subscript end subscript invisible function application x subscript 1 end subscript$ = 1

Related Questions to study

The expression logp 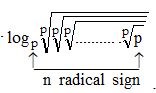where $p greater or equal than 2 comma p element of N semicolon n element of N$ when simplified is.

The expression logp where $p greater or equal than 2 comma p element of N semicolon n element of N$ when simplified is.

Let N= $open parentheses open parentheses square root of 7 close parentheses to the power of fraction numerator 2 over denominator log subscript 25 end subscript invisible function application 7 end fraction end exponent minus 12 5 to the power of log subscript 25 end subscript invisible function application 6 end exponent close parentheses$ Then log₂N has the value –

Let N= $open parentheses open parentheses square root of 7 close parentheses to the power of fraction numerator 2 over denominator log subscript 25 end subscript invisible function application 7 end fraction end exponent minus 12 5 to the power of log subscript 25 end subscript invisible function application 6 end exponent close parentheses$ Then log₂N has the value –

If a² + 4b² = 12ab, then log (a + 2b) =

If a² + 4b² = 12ab, then log (a + 2b) =

parallel

Given that log_px = α and log_qx = β, then value of log_p_/q x equals-

Given that log_px = α and log_qx = β, then value of log_p_/q x equals-

If f(x) is the primitive of $fraction numerator sin invisible function application root index 3 of x end root log invisible function application left parenthesis 1 plus 3 x right parenthesis over denominator left parenthesis tan to the power of – 1 end exponent invisible function application square root of x right parenthesis to the power of 2 end exponent left parenthesis e to the power of root index 3 of x end root end exponent – 1 right parenthesis end fraction$ (x $not equal to$ 0), then $stack l i m with x rightwards arrow 0 below$ f ' (x) is -

If f(x) is the primitive of $fraction numerator sin invisible function application root index 3 of x end root log invisible function application left parenthesis 1 plus 3 x right parenthesis over denominator left parenthesis tan to the power of – 1 end exponent invisible function application square root of x right parenthesis to the power of 2 end exponent left parenthesis e to the power of root index 3 of x end root end exponent – 1 right parenthesis end fraction$ (x $not equal to$ 0), then $stack l i m with x rightwards arrow 0 below$ f ' (x) is -

If f(x) is the primitive of $fraction numerator sin invisible function application root index 3 of x end root log invisible function application left parenthesis 1 plus 3 x right parenthesis over denominator left parenthesis tan to the power of negative 1 end exponent invisible function application square root of x right parenthesis to the power of 2 end exponent left parenthesis e to the power of root index 3 of x end root end exponent minus 1 right parenthesis end fraction$ (x $not equal to$ 0), then $stack l i m with x rightwards arrow 0 below f ´ left parenthesis x right parenthesis$ is-

If f(x) is the primitive of $fraction numerator sin invisible function application root index 3 of x end root log invisible function application left parenthesis 1 plus 3 x right parenthesis over denominator left parenthesis tan to the power of negative 1 end exponent invisible function application square root of x right parenthesis to the power of 2 end exponent left parenthesis e to the power of root index 3 of x end root end exponent minus 1 right parenthesis end fraction$ (x $not equal to$ 0), then $stack l i m with x rightwards arrow 0 below f ´ left parenthesis x right parenthesis$ is-

parallel

If $f left parenthesis x right parenthesis equals open vertical bar table row cell s i n invisible function application x end cell cell s i n invisible function application a end cell cell s i n invisible function application b end cell row cell c o s invisible function application x end cell cell c o s invisible function application a end cell cell c o s invisible function application b end cell row cell t a n invisible function application x end cell cell t a n invisible function application a end cell cell t a n invisible function application b end cell end table close vertical bar$ where $0 less than a less than b less than fraction numerator pi over denominator 2 end fraction$ hen the equation f(x) = 0 has, in the interval (a, b)

If $f left parenthesis x right parenthesis equals open vertical bar table row cell s i n invisible function application x end cell cell s i n invisible function application a end cell cell s i n invisible function application b end cell row cell c o s invisible function application x end cell cell c o s invisible function application a end cell cell c o s invisible function application b end cell row cell t a n invisible function application x end cell cell t a n invisible function application a end cell cell t a n invisible function application b end cell end table close vertical bar$ where $0 less than a less than b less than fraction numerator pi over denominator 2 end fraction$ hen the equation f(x) = 0 has, in the interval (a, b)

The velocity-time graph of a particle moving along a straight line is shown in figure. The displacement of the body in 5s is

The velocity-time graph of a particle moving along a straight line is shown in figure. The displacement of the body in 5s is

physics-General

Let f x( ) and g x( ) are defined and differentiable for $x greater or equal than x subscript 0 end subscript$ and $f open parentheses x subscript 0 close parentheses equals g open parentheses x subscript 0 close parentheses comma f to the power of ´ left parenthesis x right parenthesis greater than straight g to the power of straight prime left parenthesis x right parenthesis text for end text x greater than x subscript 0$ then

Let f x( ) and g x( ) are defined and differentiable for $x greater or equal than x subscript 0 end subscript$ and $f open parentheses x subscript 0 close parentheses equals g open parentheses x subscript 0 close parentheses comma f to the power of ´ left parenthesis x right parenthesis greater than straight g to the power of straight prime left parenthesis x right parenthesis text for end text x greater than x subscript 0$ then

parallel

In the given figure, if POQ is a diameter of the circle and PR = QR, then RPQ is

In the given figure, if POQ is a diameter of the circle and PR = QR, then RPQ is

In the given figure, find the values of ‘x’ and ‘y’

In the given figure, find the values of ‘x’ and ‘y’

PQRS is a cyclic quadrilateral and PQ is the diameter of the circle. If QPR= ° 35 , then the value of PSR is

PQRS is a cyclic quadrilateral and PQ is the diameter of the circle. If QPR= ° 35 , then the value of PSR is

parallel

Find the value of ‘x’ in the given figure

Find the value of ‘x’ in the given figure

In the given figure, find PR

In the given figure, find PR

In the given figure PA, PB, EC, FB, FD and ED are tangents to the circle. If PA=13cm,CE = 4.5cm and EF = 9cm then PF is

In the given figure PA, PB, EC, FB, FD and ED are tangents to the circle. If PA=13cm,CE = 4.5cm and EF = 9cm then PF is

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.