Maths-
General
Easy
Question
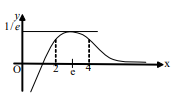
Let  then
then
Statement-1:  because
because
Statement 2 : 
- Statement-1is True, Statement-2 is True;Statement-2 is a correct explanation for Statement-1
- Statement-1 is True, Statement-2 is True;Statement-2 is not a correct explanation
- Statement -1 is True, Statement -2 is False
- Statement -1 is False, Statement -2 is True
The correct answer is: Statement-1is True, Statement-2 is True;Statement-2 is a correct explanation for Statement-1
Related Questions to study
maths-
If f(x) is a polynomial function such that  for all non zero real values of x and f(4) = -15 then f(3) + f(-3) =
for all non zero real values of x and f(4) = -15 then f(3) + f(-3) =
If f(x) is a polynomial function such that  for all non zero real values of x and f(4) = -15 then f(3) + f(-3) =
for all non zero real values of x and f(4) = -15 then f(3) + f(-3) =
maths-General
maths-
The total number of solutions of  where [.] and {.} denote greatest integer function and fractional part, respectively is equal to
where [.] and {.} denote greatest integer function and fractional part, respectively is equal to
The total number of solutions of  where [.] and {.} denote greatest integer function and fractional part, respectively is equal to
where [.] and {.} denote greatest integer function and fractional part, respectively is equal to
maths-General
maths-
Let  where
where  denotes the greatest integer smaller than or equal to x. When x is not an integer, what is f’ (x) ?
denotes the greatest integer smaller than or equal to x. When x is not an integer, what is f’ (x) ?
Let  where
where  denotes the greatest integer smaller than or equal to x. When x is not an integer, what is f’ (x) ?
denotes the greatest integer smaller than or equal to x. When x is not an integer, what is f’ (x) ?
maths-General
maths-
For  with f(1) = 2 If
with f(1) = 2 If  then the ordered pair (a, n) is
then the ordered pair (a, n) is
For  with f(1) = 2 If
with f(1) = 2 If  then the ordered pair (a, n) is
then the ordered pair (a, n) is
maths-General
maths-
Let  and
and  then
then
Let  and
and  then
then
maths-General
maths-
If functions  satisfying
satisfying  integer, are formed, then number of such functions can be
integer, are formed, then number of such functions can be
If functions  satisfying
satisfying  integer, are formed, then number of such functions can be
integer, are formed, then number of such functions can be
maths-General
maths-
Let  .Then f(f(x)) = x if α =
.Then f(f(x)) = x if α =
Let  .Then f(f(x)) = x if α =
.Then f(f(x)) = x if α =
maths-General
maths-
A = (1,2,3,4,5), B = (1,2,3,4) and  is a function. Then
is a function. Then
A = (1,2,3,4,5), B = (1,2,3,4) and  is a function. Then
is a function. Then
maths-General
maths-
The range of the function  when [.] is the greatest integer function, is
when [.] is the greatest integer function, is
The range of the function  when [.] is the greatest integer function, is
when [.] is the greatest integer function, is
maths-General
physics-
The graphs in figure show that a quantity y varies with displacement d in a system undergoing simple harmonic motion.

Which graphs best represents the relationship obtained when y is
The total energy of the system
The graphs in figure show that a quantity y varies with displacement d in a system undergoing simple harmonic motion.

Which graphs best represents the relationship obtained when y is
The total energy of the system
physics-General
physics-
A body performs simple harmonic oscillations along the straight line ABCDE with C as the midpoint of AE. Its kinetic energies at B and D are each one fourth of its maximum value. If AE = 2R, the distance between B and D is

A body performs simple harmonic oscillations along the straight line ABCDE with C as the midpoint of AE. Its kinetic energies at B and D are each one fourth of its maximum value. If AE = 2R, the distance between B and D is

physics-General
physics-
Two particles are in SHM in a straight line about same equilibrium position. Amplitude A and time period T of both the particles are equal. At time t=0, one particle is at displacement y1= +A and the other at y2= –A/2, and they are approaching towards each other. After what time they cross each other?
Two particles are in SHM in a straight line about same equilibrium position. Amplitude A and time period T of both the particles are equal. At time t=0, one particle is at displacement y1= +A and the other at y2= –A/2, and they are approaching towards each other. After what time they cross each other?
physics-General
physics-
A semicircle conducting ring of radius R is placed in the xy plane, as shown in the figure. A uniform magnetic field is set up along the x–axis. No emf, will be induced in the ring. If

A semicircle conducting ring of radius R is placed in the xy plane, as shown in the figure. A uniform magnetic field is set up along the x–axis. No emf, will be induced in the ring. If

physics-General
physics-
Two wedges, each of mass m, are placed next to each other on a flat floor. A cube of mass M is balanced on the wedges as shown. Assume no friction between the cube and the wedges, but a coefficient of static friction  between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges?
between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges?

Two wedges, each of mass m, are placed next to each other on a flat floor. A cube of mass M is balanced on the wedges as shown. Assume no friction between the cube and the wedges, but a coefficient of static friction  between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges?
between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges?

physics-General
physics-
A string is wrapped round a log of wood and it is pulled with a force F as shown in the figure.Choose the correct statement(s).
I Tension T in the string decreases with increase in  , II Tension
, II Tension 

A string is wrapped round a log of wood and it is pulled with a force F as shown in the figure.Choose the correct statement(s).
I Tension T in the string decreases with increase in  , II Tension
, II Tension 

physics-General