Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

Let $x to the power of 2 end exponent not equal to n pi minus 1 comma n element of N$ , then $integral x square root of fraction numerator 2 s i n invisible function application open parentheses x to the power of 2 end exponent plus 1 close parentheses minus s i n invisible function application 2 open parentheses x to the power of 2 end exponent plus 1 close parentheses over denominator 2 s i n invisible function application open parentheses x to the power of 2 end exponent plus 1 close parentheses plus s i n invisible function application 2 open parentheses x to the power of 2 end exponent plus 1 close parentheses end fraction end root d x$ is equal to:

$l n |\frac{1}{2} s e c (x^{2} + 1)| + C$
$l n |s e c (\frac{x^{2} + 1}{2})| + C$
$- \frac{8}{3} \ln | (1 - x) | + \frac{2}{3} x + c$
$\frac{1}{2} l n |\frac{2}{s e c (x^{2} + 1)}| + C$

The correct answer is: $l n invisible function application open vertical bar s e c invisible function application open parentheses fraction numerator x to the power of 2 end exponent plus 1 over denominator 2 end fraction close parentheses close vertical bar plus C$

Related Questions to study

Statement I : y = f(x) = $fraction numerator x to the power of 2 end exponent minus 2 x plus 4 over denominator x to the power of 2 end exponent minus 2 x plus 5 end fraction$ , x $element of$ R Range of f(x) is [3/4, 1)
Statement II : $left parenthesis x minus 1 right parenthesis to the power of 2 end exponent equals fraction numerator 4 y minus 3 over denominator 1 minus y end fraction$ .

Statement I : y = f(x) = $fraction numerator x to the power of 2 end exponent minus 2 x plus 4 over denominator x to the power of 2 end exponent minus 2 x plus 5 end fraction$ , x $element of$ R Range of f(x) is [3/4, 1)
Statement II : $left parenthesis x minus 1 right parenthesis to the power of 2 end exponent equals fraction numerator 4 y minus 3 over denominator 1 minus y end fraction$ .

Statement I : Function f(x) = sinx + {x} is periodic with period $2 pi$
Statement II : sin x and {x} are both periodic with period $2 pi$ and 1 respectively.

Statement I : Function f(x) = sinx + {x} is periodic with period $2 pi$
Statement II : sin x and {x} are both periodic with period $2 pi$ and 1 respectively.

Statement 1 : f : R $rightwards arrow$ R and $f left parenthesis x right parenthesis equals e to the power of x end exponent plus e to the power of negative x end exponent$ is bijective.
Statement 2 : $f colon R rightwards arrow R comma space f left parenthesis x right parenthesis equals e to the power of x minus e to the power of negative x end exponent$ is bijective.

Statement 1 : f : R $rightwards arrow$ R and $f left parenthesis x right parenthesis equals e to the power of x end exponent plus e to the power of negative x end exponent$ is bijective.
Statement 2 : $f colon R rightwards arrow R comma space f left parenthesis x right parenthesis equals e to the power of x minus e to the power of negative x end exponent$ is bijective.

parallel

Statement I : Graph of y = tan x is symmetrical about origin
Statement II : Graph of $y equals sec squared invisible function application x$ is symmetrical about y-axis

Statement I : Graph of y = tan x is symmetrical about origin
Statement II : Graph of $y equals sec squared invisible function application x$ is symmetrical about y-axis

Statement- $1 colon$ If $f left parenthesis x right parenthesis equals vertical line x minus 1 vertical line plus vertical line x minus 2 vertical line plus vertical line x minus 3 vertical line$ Where $2 less than x less than 3$ is an identity function.
Statement- $2 colon f colon A rightwards arrow$ R defined by $f left parenthesis x right parenthesis equals x$ is an identity function.

Statement- $1 colon$ If $f left parenthesis x right parenthesis equals vertical line x minus 1 vertical line plus vertical line x minus 2 vertical line plus vertical line x minus 3 vertical line$ Where $2 less than x less than 3$ is an identity function.
Statement- $2 colon f colon A rightwards arrow$ R defined by $f left parenthesis x right parenthesis equals x$ is an identity function.

Assertion (A) : 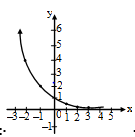Graph of $open curly brackets left parenthesis x comma y right parenthesis divided by y equals 2 to the power of negative x end exponent text and end text x comma y element of R close curly brackets$
Reason (R) : In the expression a^m/n, where a, m, n × J⁺, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.

Assertion (A) : Graph of $open curly brackets left parenthesis x comma y right parenthesis divided by y equals 2 to the power of negative x end exponent text and end text x comma y element of R close curly brackets$
Reason (R) : In the expression a^m/n, where a, m, n × J⁺, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.

parallel

Assertion: The period of $f left parenthesis x right parenthesis equals s i n invisible function application 2 x c o s invisible function application left square bracket 2 x right square bracket minus c o s invisible function application 2 x s i n invisible function application left square bracket 2 x right square bracket$ is 1/2.
Reason: The period of x – [x] is 1.

Assertion: The period of $f left parenthesis x right parenthesis equals s i n invisible function application 2 x c o s invisible function application left square bracket 2 x right square bracket minus c o s invisible function application 2 x s i n invisible function application left square bracket 2 x right square bracket$ is 1/2.
Reason: The period of x – [x] is 1.

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion: The function defined by $f left parenthesis x right parenthesis equals x to the power of 3 end exponent plus a x to the power of 2 end exponent plus b x plus c$ is invertible if and only if $a to the power of 2 end exponent less or equal than 3 b$ .
Reason: A function is invertible if and only if it is one-to-one and onto function.

Assertion: The function defined by $f left parenthesis x right parenthesis equals x to the power of 3 end exponent plus a x to the power of 2 end exponent plus b x plus c$ is invertible if and only if $a to the power of 2 end exponent less or equal than 3 b$ .
Reason: A function is invertible if and only if it is one-to-one and onto function.

parallel

Assertion : $f left parenthesis x right parenthesis equals s g n left parenthesis x minus vertical line x vertical line right parenthesis$ can never become positive.
Reason : f(x) = sgn x is always a positive function.

Assertion : $f left parenthesis x right parenthesis equals s g n left parenthesis x minus vertical line x vertical line right parenthesis$ can never become positive.
Reason : f(x) = sgn x is always a positive function.

If f (x) = $open curly brackets table row cell e to the power of cos invisible function application x end exponent end cell cell sin invisible function application x text for end text vertical line x vertical line less or equal than 2 end cell row cell text 2, end text end cell cell text otherwise end text end cell end table comma text then end text not stretchy integral subscript text -2 end text end subscript superscript 3 end superscript f left parenthesis x right parenthesis d x equals close$

If f (x) = $open curly brackets table row cell e to the power of cos invisible function application x end exponent end cell cell sin invisible function application x text for end text vertical line x vertical line less or equal than 2 end cell row cell text 2, end text end cell cell text otherwise end text end cell end table comma text then end text not stretchy integral subscript text -2 end text end subscript superscript 3 end superscript f left parenthesis x right parenthesis d x equals close$

The value of the integral $not stretchy integral subscript e to the power of negative 1 end exponent end subscript superscript e to the power of 2 end exponent end superscript open vertical bar fraction numerator log subscript e end subscript invisible function application blank x over denominator x end fraction close vertical bar$ dx is :

The value of the integral $not stretchy integral subscript e to the power of negative 1 end exponent end subscript superscript e to the power of 2 end exponent end superscript open vertical bar fraction numerator log subscript e end subscript invisible function application blank x over denominator x end fraction close vertical bar$ dx is :

parallel

Assertion : Let $f colon R minus left curly bracket 1 , 2 comma 3 right curly bracket rightwards arrow R$ be a function defined by f(x) = $fraction numerator 1 over denominator x minus 1 end fraction plus fraction numerator 2 over denominator x minus 2 end fraction plus fraction numerator 3 over denominator x minus 3 end fraction$ . Then f is many-one function.
Reason : If either $f apostrophe left parenthesis x right parenthesis greater than 0$ or $f to the power of apostrophe left parenthesis x right parenthesis less than 0 comma for all x element of$ domain of f, then y = f(x) is one-one function.</span

Assertion : Let $f colon R minus left curly bracket 1 , 2 comma 3 right curly bracket rightwards arrow R$ be a function defined by f(x) = $fraction numerator 1 over denominator x minus 1 end fraction plus fraction numerator 2 over denominator x minus 2 end fraction plus fraction numerator 3 over denominator x minus 3 end fraction$ . Then f is many-one function.
Reason : If either $f apostrophe left parenthesis x right parenthesis greater than 0$ or $f to the power of apostrophe left parenthesis x right parenthesis less than 0 comma for all x element of$ domain of f, then y = f(x) is one-one function.</span

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Assertion : Fundamental period of $c o s invisible function application x plus c o t invisible function application x text is end text 2 pi$ .
Reason : If the period of f(x) is $T subscript 1 end subscript$ and the period of g(x) is $T subscript 2 end subscript$ , then the fundamental period of f(x) + g(x) is the L.C.M. of $T subscript 1 end subscript$ and T

Function $f colon Z rightwards arrow Z comma$ f(x) = 2x + 1 is-

Function $f colon Z rightwards arrow Z comma$ f(x) = 2x + 1 is-

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.