Maths-
General
Easy
Question
The curve  touches the
touches the  ‐axis at P(-2,0) and cuts the y ‐axis at a point
‐axis at P(-2,0) and cuts the y ‐axis at a point  where its gradient is 3 Then a+2b+c=-
where its gradient is 3 Then a+2b+c=-



- 1
The correct answer is: 1
Since the curve  touches x‐ axis at
touches x‐ axis at  then x‐ axis is the tangent at
then x‐ axis is the tangent at  The curve meets
The curve meets  ‐axis in
‐axis in  We have
We have

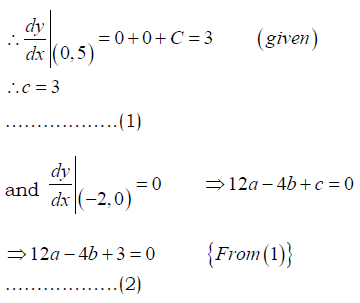
and  lies on the curve then
lies on the curve then


 (3)
(3)
From (2) and (3) we get 
Hence 

Related Questions to study
maths-
If  is to be square root of a determinant of the two rowed unit matrix, then
is to be square root of a determinant of the two rowed unit matrix, then 
 should satisfy the relation
should satisfy the relation
If  is to be square root of a determinant of the two rowed unit matrix, then
is to be square root of a determinant of the two rowed unit matrix, then 
 should satisfy the relation
should satisfy the relation
maths-General
maths-
Matrix Ais given by  then the determinant of
then the determinant of  is
is
Matrix Ais given by  then the determinant of
then the determinant of  is
is
maths-General
maths-
If  then
then 
If  then
then 
maths-General
maths-
If  then the number of positive divisors of the number p is
then the number of positive divisors of the number p is
If  then the number of positive divisors of the number p is
then the number of positive divisors of the number p is
maths-General
maths-
The number of positive integral solutions of the equation  is
is
The number of positive integral solutions of the equation  is
is
maths-General
maths-
If 


 be real matrices (not necessasrily square) such that
be real matrices (not necessasrily square) such that 


 forthematrix
forthematrix  consider the statements
consider the statements 

If 


 be real matrices (not necessasrily square) such that
be real matrices (not necessasrily square) such that 


 forthematrix
forthematrix  consider the statements
consider the statements 

maths-General
maths-
If  , then
, then
Statement  because
because
Statement  :A.M
:A.M  for
for 
If  , then
, then
Statement  because
because
Statement  :A.M
:A.M  for
for 
maths-General
maths-
If  , then the value of
, then the value of  is equal to
is equal to
If  , then the value of
, then the value of  is equal to
is equal to
maths-General
maths-
The minimum value of  is
is
The minimum value of  is
is
maths-General
maths-
If  andy
andy  (x)then
(x)then  at x=1 is
at x=1 is
If  andy
andy  (x)then
(x)then  at x=1 is
at x=1 is
maths-General
maths-
Statement 1:Degree of differential equation  is not defined
is not defined
Statement 2: In the given D.E, the power of highest order derivative when expressed as a polynomials of derivatives is called degree
Statement 1:Degree of differential equation  is not defined
is not defined
Statement 2: In the given D.E, the power of highest order derivative when expressed as a polynomials of derivatives is called degree
maths-General
maths-
The solution of  is
is
The solution of  is
is
maths-General
maths-
Solution of the equation  is
is  ( where c is arbitrary constant)
( where c is arbitrary constant)
Solution of the equation  is
is  ( where c is arbitrary constant)
( where c is arbitrary constant)
maths-General
Maths-
Assertion (A) : If (2, 3) and (3,2) are respectively the orthocenters of  and
and  where D, E, F are mid points of sides of
where D, E, F are mid points of sides of  respectively then the centroid of either triangle is
respectively then the centroid of either triangle is 
Reason (R) :Circumcenters of triangles formed by mid‐points of sides of  and pedal triangle of
and pedal triangle of  are same
are same
Assertion (A) : If (2, 3) and (3,2) are respectively the orthocenters of  and
and  where D, E, F are mid points of sides of
where D, E, F are mid points of sides of  respectively then the centroid of either triangle is
respectively then the centroid of either triangle is 
Reason (R) :Circumcenters of triangles formed by mid‐points of sides of  and pedal triangle of
and pedal triangle of  are same
are same
Maths-General
physics-
Two metallic strings A and B of different materials are connected in series forming a joint. The strings have similar cross-sectional area. The length of A is  and that of B is
and that of B is  . One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass m passing over a frictionless pulley. Transverse waves are setup in the combined string using an external source of variable frequency. The total number of antinodes at this frequency with joint as node is (the densities of A and B are
. One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass m passing over a frictionless pulley. Transverse waves are setup in the combined string using an external source of variable frequency. The total number of antinodes at this frequency with joint as node is (the densities of A and B are  respectively)
respectively)
Two metallic strings A and B of different materials are connected in series forming a joint. The strings have similar cross-sectional area. The length of A is  and that of B is
and that of B is  . One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass m passing over a frictionless pulley. Transverse waves are setup in the combined string using an external source of variable frequency. The total number of antinodes at this frequency with joint as node is (the densities of A and B are
. One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass m passing over a frictionless pulley. Transverse waves are setup in the combined string using an external source of variable frequency. The total number of antinodes at this frequency with joint as node is (the densities of A and B are  respectively)
respectively)
physics-General





