Question
A particle of mass 
is initially situated at the point 
inside a hemispherical surface of radius 
as shown in figure. A horizontal acceleration of magnitude
is suddenly produced on the particle in the horizontal direction. If gravitational acceleration is neglected, the time taken by particle to touch the sphere again is
- None of these
The correct answer is:
Let the particle touches the sphere t the point 
Let 
In 
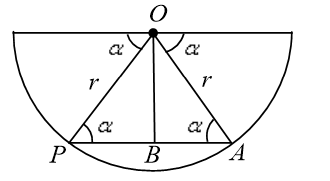
or 
Related Questions to study
A cyclist starts from the centre
of a circular park of radius 1 km, reaches the edge of the park, then cycles along the circumference and returns to the point as shown in figure. If the round trip takes 10 min, the net displacement and average speed of the cyclist (in metre and kilometer per hour) are
A cyclist starts from the centre of a circular park of radius 1 km, reaches the edge of the park, then cycles along the circumference and returns to the point as shown in figure. If the round trip takes 10 min, the net displacement and average speed of the cyclist (in metre and kilometer per hour) are
A the instant a motor bike starts from rest in a given direction, a car overtakes the motor bike, both moving in the same direction. The speed-time graphs for motor bike and car are represented by 
and 
respectively Then
A the instant a motor bike starts from rest in a given direction, a car overtakes the motor bike, both moving in the same direction. The speed-time graphs for motor bike and car are represented by and respectively Then
Assertion : Owls can move freely during night.
Reason : They have large number of rods on their retina.
Assertion : Owls can move freely during night.
Reason : They have large number of rods on their retina.
A particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point
A particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point
The area bounded by y=3x and 
is
So now here we can say that using the integration method, the area of the region bounded by the given curves is 4.5. The equation A = ∫ab f(x) dx gives the area under the curve y = f(x) and x-axis. The bounding values for the curve with respect to the x-axis are shown here as a and b.
The area bounded by y=3x and is
So now here we can say that using the integration method, the area of the region bounded by the given curves is 4.5. The equation A = ∫ab f(x) dx gives the area under the curve y = f(x) and x-axis. The bounding values for the curve with respect to the x-axis are shown here as a and b.
The area bounded by 
X- axis, x=1 and x=2 is
So now here we can say that using the integration method, the area of the region bounded by the given curve and the lines is 13/3. The equation A = ∫ab f(x) dx gives the area under the curve y = f(x) and x-axis. The bounding values for the curve with respect to the x-axis are shown here as a and b.
The area bounded by X- axis, x=1 and x=2 is
So now here we can say that using the integration method, the area of the region bounded by the given curve and the lines is 13/3. The equation A = ∫ab f(x) dx gives the area under the curve y = f(x) and x-axis. The bounding values for the curve with respect to the x-axis are shown here as a and b.
If 
then 
=
If then =
The 
graph shown in the figure represents
The graph shown in the figure represents
For the velocity-time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the seven seconds
For the velocity-time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the seven seconds
A particle starts from rest at 
and undergoes an acceleration 
in 
with time 
in second which is as shownWhich one of the following plot represents velocity 
in 
time in second?
A particle starts from rest at and undergoes an acceleration in with time in second which is as shownWhich one of the following plot represents velocity in time in second?
A body is at rest at 
. At , it starts moving in the positive 
-direction with a constant acceleration. At the same instant another body passes through moving in the positive -direction with a constant speed. The position of the first body is given by 
after time ‘’ and that of the second body by 
after the same time interval. Which of the following graphs correctly describes 
as a function of time ‘’
A body is at rest at . At , it starts moving in the positive -direction with a constant acceleration. At the same instant another body passes through moving in the positive -direction with a constant speed. The position of the first body is given by after time ‘’ and that of the second body by after the same time interval. Which of the following graphs correctly describes as a function of time ‘’
General solution of 
is
General solution of is
In the following graph, distance travelled by the body in metres is
In the following graph, distance travelled by the body in metres is
Velocity-time 
graph for a moving object is shown in the figure. Total displacement of the object during the time interval when there is non-zero acceleration and retardation is
Velocity-time graph for a moving object is shown in the figure. Total displacement of the object during the time interval when there is non-zero acceleration and retardation is
The value of k such that 
lies in the plane 2x-4y+z+7=0 is
So here we used the concept of three dimensional geometry to understand and solve the question. Any point's position or coordinates in 3D space are determined by how far they have travelled along the x, y, and z axes, respectively. So here the value of k is 7.
The value of k such that lies in the plane 2x-4y+z+7=0 is
So here we used the concept of three dimensional geometry to understand and solve the question. Any point's position or coordinates in 3D space are determined by how far they have travelled along the x, y, and z axes, respectively. So here the value of k is 7.
