Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

A string of length $L$ is fixed at one end and carries a mass $M$ at the other end. The string makes $2 divided by pi$ revolutions per $s e c o n d$ around the vertical axis through the fixed end as shown in figure, then tension in the string is

$M L$
$2 M L$
$4 M L$
$16 M L$

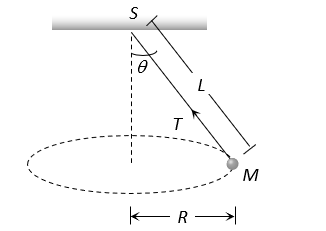
The correct answer is: $16 blank M L$

$T sin invisible function application theta equals M omega to the power of 2 end exponent R$ (i)
$T sin invisible function application theta equals M omega to the power of 2 end exponent L sin invisible function application theta$ (ii)
From (i) and (ii)
$T equals M omega to the power of 2 end exponent L$
$equals M blank 4 pi to the power of 2 end exponent n to the power of 2 end exponent L$
$equals M blank 4 pi to the power of 2 end exponent open parentheses fraction numerator 2 over denominator pi end fraction close parentheses to the power of 2 end exponent L equals 16 blank M L$

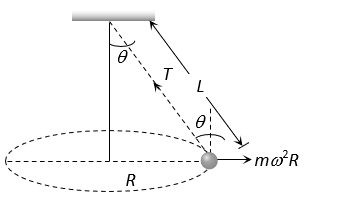
Related Questions to study

$cos invisible function application left parenthesis alpha minus beta right parenthesis equals 1 text and end text cos invisible function application left parenthesis alpha plus beta right parenthesis equals 1 over c$ where $alpha comma beta element of left square bracket negative pi comma pi right square bracket$ Pairs $alpha comma beta$ which satisfy both the equations is/are

$cos invisible function application left parenthesis alpha minus beta right parenthesis equals 1 text and end text cos invisible function application left parenthesis alpha plus beta right parenthesis equals 1 over c$ where $alpha comma beta element of left square bracket negative pi comma pi right square bracket$ Pairs $alpha comma beta$ which satisfy both the equations is/are

The number of integral values of k for which the equation $7 cos invisible function application x plus 5 sin invisible function application x equals 2 k plus 1$ has a solution is

The number of integral values of k for which the equation $7 cos invisible function application x plus 5 sin invisible function application x equals 2 k plus 1$ has a solution is

The number of distinct real roots of $open vertical bar table attributes columnalign center center center columnspacing 1em end attributes row cell sin invisible function application x end cell cell cos invisible function application x end cell cell cos invisible function application x end cell row cell cos invisible function application x end cell cell sin invisible function application x end cell cell cos invisible function application x end cell row cell cos invisible function application x end cell cell cos invisible function application x end cell cell sin invisible function application x end cell end table close vertical bar equals 0$ in the interval $negative pi over 4 less or equal than x less or equal than pi over 4$ is

The number of distinct real roots of $open vertical bar table attributes columnalign center center center columnspacing 1em end attributes row cell sin invisible function application x end cell cell cos invisible function application x end cell cell cos invisible function application x end cell row cell cos invisible function application x end cell cell sin invisible function application x end cell cell cos invisible function application x end cell row cell cos invisible function application x end cell cell cos invisible function application x end cell cell sin invisible function application x end cell end table close vertical bar equals 0$ in the interval $negative pi over 4 less or equal than x less or equal than pi over 4$ is

parallel

If $0 less or equal than x less than 2 pi$ , then the number of real values of x, which satisfy the equation $cos invisible function application x plus cos invisible function application 2 x plus cos invisible function application 3 x plus cos invisible function application 4 x equals 0$ is :

If $0 less or equal than x less than 2 pi$ , then the number of real values of x, which satisfy the equation $cos invisible function application x plus cos invisible function application 2 x plus cos invisible function application 3 x plus cos invisible function application 4 x equals 0$ is :

The number of solutions of the equation $cos squared invisible function application open parentheses x plus pi over 6 close parentheses plus cos squared invisible function application x minus 2 cos invisible function application open parentheses x plus pi over 6 close parentheses cos invisible function application open parentheses pi over 6 close parentheses equals sin squared invisible function application pi over 6$ in the interval $left parenthesis negative pi divided by 2 comma pi divided by 2 right parenthesis$ is

The number of solutions of the equation $cos squared invisible function application open parentheses x plus pi over 6 close parentheses plus cos squared invisible function application x minus 2 cos invisible function application open parentheses x plus pi over 6 close parentheses cos invisible function application open parentheses pi over 6 close parentheses equals sin squared invisible function application pi over 6$ in the interval $left parenthesis negative pi divided by 2 comma pi divided by 2 right parenthesis$ is

The possible values of $theta element of left parenthesis 0 comma pi right parenthesis$ such that $sin invisible function application theta plus sin invisible function application 4 theta plus sin invisible function application 7 theta equals 0$ are :

The possible values of $theta element of left parenthesis 0 comma pi right parenthesis$ such that $sin invisible function application theta plus sin invisible function application 4 theta plus sin invisible function application 7 theta equals 0$ are :

parallel

The number of values of x in the interval [0, 3 $straight pi$ ] satisfying the equation , $2 sin squared invisible function application x plus 5 sin invisible function application x minus 3 equals 0$ is

The number of values of x in the interval [0, 3 $straight pi$ ] satisfying the equation , $2 sin squared invisible function application x plus 5 sin invisible function application x minus 3 equals 0$ is

The number of solutions of tan x + sec x = 2 cos x in [0, 2 $straight pi$ ], is

The number of solutions of tan x + sec x = 2 cos x in [0, 2 $straight pi$ ], is

Over $left square bracket negative pi comma pi right square bracket$ the solution of $2 sin squared invisible function application open parentheses x plus pi over 4 close parentheses plus square root of 3 cos invisible function application 2 x greater or equal than 0$ is

Over $left square bracket negative pi comma pi right square bracket$ the solution of $2 sin squared invisible function application open parentheses x plus pi over 4 close parentheses plus square root of 3 cos invisible function application 2 x greater or equal than 0$ is

parallel

Solution to inequality cos 2x + 5 cos x + 3 ≥ 0 over $left square bracket negative pi comma pi right square bracket$ is

Solution to inequality cos 2x + 5 cos x + 3 ≥ 0 over $left square bracket negative pi comma pi right square bracket$ is

Let $f left parenthesis x right parenthesis equals fraction numerator c o s e c to the power of 4 end exponent invisible function application x minus 2 c o s e c to the power of 2 end exponent invisible function application x plus 1 over denominator c o s e c invisible function application x left parenthesis c o s e c invisible function application x minus s i n invisible function application x right parenthesis plus fraction numerator s i n invisible function application x minus c o s invisible function application x over denominator sin invisible function application x end fraction plus c o t invisible function application x end fraction$ The sum of all the solutions of f (x) = 0 in [0, 100p] is

Let $f left parenthesis x right parenthesis equals fraction numerator c o s e c to the power of 4 end exponent invisible function application x minus 2 c o s e c to the power of 2 end exponent invisible function application x plus 1 over denominator c o s e c invisible function application x left parenthesis c o s e c invisible function application x minus s i n invisible function application x right parenthesis plus fraction numerator s i n invisible function application x minus c o s invisible function application x over denominator sin invisible function application x end fraction plus c o t invisible function application x end fraction$ The sum of all the solutions of f (x) = 0 in [0, 100p] is

The general solution of the trigonometric equation tan x + tan 2x + tan 3x = tan x · tan 2x tan 3x is
where n $element of$ I

The general solution of the trigonometric equation tan x + tan 2x + tan 3x = tan x · tan 2x tan 3x is
where n $element of$ I

parallel

The sum of all the solution of cotθ= sin 2θ(θ ≠ n $straight pi$ , n integer), 0 , $less or equal than theta less or equal than pi$ is

The sum of all the solution of cotθ= sin 2θ(θ ≠ n $straight pi$ , n integer), 0 , $less or equal than theta less or equal than pi$ is

$L t subscript x not stretchy rightwards arrow 0 end subscript fraction numerator left parenthesis 1 plus x right parenthesis to the power of 1 fifth end exponent minus left parenthesis 1 minus x right parenthesis to the power of 1 half end exponent over denominator x end fraction$

$L t subscript x not stretchy rightwards arrow 0 end subscript fraction numerator left parenthesis 1 plus x right parenthesis to the power of 1 fifth end exponent minus left parenthesis 1 minus x right parenthesis to the power of 1 half end exponent over denominator x end fraction$

$L t subscript x not stretchy rightwards arrow 0 end subscript fraction numerator sin space open parentheses pi cos squared space x close parentheses over denominator x squared end fraction$

$L t subscript x not stretchy rightwards arrow 0 end subscript fraction numerator sin space open parentheses pi cos squared space x close parentheses over denominator x squared end fraction$

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.