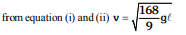Question
A thin rod of mass m and length  is hinged to a ceiling and it is free to rotate in a vertical plane. A particle of mass m, moving with speed v strikes it as shown in the figure and gets stick with the rod. The value of v , for which the rod becomes horizontal after collision is
is hinged to a ceiling and it is free to rotate in a vertical plane. A particle of mass m, moving with speed v strikes it as shown in the figure and gets stick with the rod. The value of v , for which the rod becomes horizontal after collision is

- The value of v, for which rod becomes horizontal after collision is

- The value of v, for which rod becomes horizontal after collision is

- Angular momentum of (rod + particle) system will remain constant about hinge just before and after collision
- Angular momentum of (rod + particle) system will remain same about centre of mass just before and after collision
The correct answer is: The value of v, for which rod becomes horizontal after collision is 
Related Questions to study
An impulsive force F acts horizontally on a solid sphere of radius R placed on a horizontal surface. The line of action of the impulsive force is at a height h above the centre of the sphere. If the rotational and translational kinetic energies of the sphere just after the impulse are equal, then the value of h will be

An impulsive force F acts horizontally on a solid sphere of radius R placed on a horizontal surface. The line of action of the impulsive force is at a height h above the centre of the sphere. If the rotational and translational kinetic energies of the sphere just after the impulse are equal, then the value of h will be

The disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then

The disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then

The figure shows a uniform rod lying along the x-axis. The locus of all the points lying on the xy-plane, about which the moment of inertia of the rod is same as that about O is :

The figure shows a uniform rod lying along the x-axis. The locus of all the points lying on the xy-plane, about which the moment of inertia of the rod is same as that about O is :

Figure shows a uniform disk, with mass M = 2.4 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block of mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. The tension in cord is

Figure shows a uniform disk, with mass M = 2.4 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block of mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. The tension in cord is

A small block of mass 'm' is rigidly attached at 'P' to a ring of mass '3m' and radius 'r'. The system is released from rest at  and rolls without sliding. The angular acceleration of hoop just after release is
and rolls without sliding. The angular acceleration of hoop just after release is

A small block of mass 'm' is rigidly attached at 'P' to a ring of mass '3m' and radius 'r'. The system is released from rest at  and rolls without sliding. The angular acceleration of hoop just after release is
and rolls without sliding. The angular acceleration of hoop just after release is

x – 2 = t2, y = 2t are the parametric equations of the parabola
parametric form gives us the general coordinates of the curve. we can solve for the two to build the relationship between the x and y coordinates which gives us the locus
x – 2 = t2, y = 2t are the parametric equations of the parabola
parametric form gives us the general coordinates of the curve. we can solve for the two to build the relationship between the x and y coordinates which gives us the locus
Vertex of the parabola y2 + 2y + x = 0 lies in the quadrant
vertex of the parabola is the point that divides the curve into two symmetric parts.
Vertex of the parabola y2 + 2y + x = 0 lies in the quadrant
vertex of the parabola is the point that divides the curve into two symmetric parts.
The equation of the parabola with focus (3, 0) and the directrix x + 3 = 0 is
the locus of all points which are equidistant from a point called focus and a aline called directrix is known as a parabola. as per this definition, we can solve the given question.
The equation of the parabola with focus (3, 0) and the directrix x + 3 = 0 is
the locus of all points which are equidistant from a point called focus and a aline called directrix is known as a parabola. as per this definition, we can solve the given question.