Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

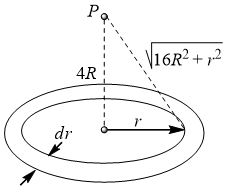
A thin uniform annular disc (see figure) of mass $M$ has outer radius $4 R$ and inner radius $3 R$ . The work required to take a unit mass from point $P$ on its axis to infinity is

$\frac{2 G M}{7 R} (4 \sqrt{2} - 5)$
$- \frac{2 G M}{7 R} (4 \sqrt{2} - 5)$
$\frac{G M}{4 R}$
$\frac{2 G M}{5 R} (\sqrt{2} - 1)$

The correct answer is: $fraction numerator 2 G M over denominator 7 R end fraction left parenthesis 4 square root of 2 minus 5 right parenthesis$

$W equals increment U equals U subscript f end subscript minus U subscript i end subscript equals U subscript infinity end subscript minus U subscript P end subscript$
$equals negative U subscript P end subscript equals negative m V subscript P end subscript$
$equals negative V subscript P end subscript open parentheses a s blank m equals 1 close parentheses$
Potential at point $P$ will be obtained by in integration as given below. Let $d M$ be the mass of small rings as shown

$d M equals fraction numerator M over denominator pi left parenthesis 4 R right parenthesis to the power of 2 end exponent minus pi left parenthesis 3 R right parenthesis to the power of 2 end exponent end fraction open parentheses 2 pi r close parentheses d r$
$equals fraction numerator 2 M r d r over denominator 7 R to the power of 2 end exponent end fraction$
$d V subscript P end subscript equals negative fraction numerator G. d M over denominator square root of 16 R to the power of 2 end exponent plus r to the power of 2 end exponent end root end fraction$
$equals negative fraction numerator 2 G M over denominator 7 R to the power of 2 end exponent end fraction not stretchy integral subscript 3 R end subscript superscript 4 R end superscript fraction numerator r over denominator square root of 16 R to the power of 2 end exponent plus r to the power of 2 end exponent end root end fraction bullet d r$
$equals negative fraction numerator 2 G M over denominator 7 R end fraction open parentheses 4 square root of 2 minus 5 close parentheses$
$therefore W equals plus fraction numerator 2 G M over denominator 7 R end fraction left parenthesis 4 square root of 2 minus 5 right parenthesis$

Related Questions to study

The two bodies of mass $m subscript 1 end subscript$ and $m subscript 2 end subscript left parenthesis m subscript 1 end subscript greater than m subscript 2 end subscript right parenthesis$ respectively are tied to the ends of a massless string, which passes over a light and frictionless pulley. The masses are initially at rest and the released. Then acceleration of the centre of mass of the system is

The two bodies of mass $m subscript 1 end subscript$ and $m subscript 2 end subscript left parenthesis m subscript 1 end subscript greater than m subscript 2 end subscript right parenthesis$ respectively are tied to the ends of a massless string, which passes over a light and frictionless pulley. The masses are initially at rest and the released. Then acceleration of the centre of mass of the system is

physics-General

If $x equals 1 plus 3 a plus 6 a squared plus 10 a cubed plus midline horizontal ellipsis.$ to $straight infinity$ terms, $vertical line a vertical line less than 1 comma y equals 1 plus 4 a plus 10 a squared plus 20 a cubed plus midline horizontal ellipsis$ $straight infinity$ terms, $vertical line a vertical line less than 1$ , then $x colon y$

If $x equals 1 plus 3 a plus 6 a squared plus 10 a cubed plus midline horizontal ellipsis.$ to $straight infinity$ terms, $vertical line a vertical line less than 1 comma y equals 1 plus 4 a plus 10 a squared plus 20 a cubed plus midline horizontal ellipsis$ $straight infinity$ terms, $vertical line a vertical line less than 1$ , then $x colon y$

The coefficient of $x to the power of negative n end exponent$ in $left parenthesis 1 plus x right parenthesis to the power of n end exponent open parentheses 1 plus fraction numerator 1 over denominator x end fraction close parentheses to the power of n end exponent$ is

The coefficient of $x to the power of negative n end exponent$ in $left parenthesis 1 plus x right parenthesis to the power of n end exponent open parentheses 1 plus fraction numerator 1 over denominator x end fraction close parentheses to the power of n end exponent$ is

parallel

$open parentheses 1 plus x plus x squared plus horizontal ellipsis plus x to the power of p close parentheses to the power of n equals a subscript 0 plus a subscript 1 x plus a subscript 2 x squared plus horizontal ellipsis$ $plus a subscript n p end subscript x to the power of n p end exponent not stretchy rightwards double arrow a subscript 1 plus 2 a subscript 2 plus 3 a subscript 3 plus horizontal ellipsis plus n p$

$open parentheses 1 plus x plus x squared plus horizontal ellipsis plus x to the power of p close parentheses to the power of n equals a subscript 0 plus a subscript 1 x plus a subscript 2 x squared plus horizontal ellipsis$ $plus a subscript n p end subscript x to the power of n p end exponent not stretchy rightwards double arrow a subscript 1 plus 2 a subscript 2 plus 3 a subscript 3 plus horizontal ellipsis plus n p$

Compounds (A) and (B) are –

Compounds (A) and (B) are –

chemistry-General

$2 times C subscript 0 plus 5 times C subscript 1 plus 8 times C subscript 2 plus horizontal ellipsis plus left parenthesis 2 plus 3 n right parenthesis times C subscript n equals$

$2 times C subscript 0 plus 5 times C subscript 1 plus 8 times C subscript 2 plus horizontal ellipsis plus left parenthesis 2 plus 3 n right parenthesis times C subscript n equals$

parallel

A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of length 3, 4 and 5 units. Then area of the triangle is equal to:

A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of length 3, 4 and 5 units. Then area of the triangle is equal to:

If one root of the equation $a x squared plus b x plus c equals 0$ is reciprocal of the one of the roots of equation $a subscript 1 x squared plus b subscript 1 x plus c subscript 1 equals 0$ then

If one root of the equation $a x squared plus b x plus c equals 0$ is reciprocal of the one of the roots of equation $a subscript 1 x squared plus b subscript 1 x plus c subscript 1 equals 0$ then

If the quadratic equation $a x squared plus 2 c x plus b equals 0$ and $a x squared plus 2 b x plus c equals 0 left parenthesis b not equal to c right parenthesis$ have a common root then $a plus 4 b plus 4 c$ is equal to

If the quadratic equation $a x squared plus 2 c x plus b equals 0$ and $a x squared plus 2 b x plus c equals 0 left parenthesis b not equal to c right parenthesis$ have a common root then $a plus 4 b plus 4 c$ is equal to

parallel

Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on frictionless horizontal surface. An impulsive force gives a velocity of 14 $m s to the power of negative 1 end exponent$ to the heavier block in the direction of the lighter block. The velocity of centre of mass of the system at that very moment is

Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on frictionless horizontal surface. An impulsive force gives a velocity of 14 $m s to the power of negative 1 end exponent$ to the heavier block in the direction of the lighter block. The velocity of centre of mass of the system at that very moment is

physics-General

In a Δabc if b+c=3a then $cot invisible function application straight B over 2 times cot invisible function application straight C over 2$ has the value equal to –

In a Δabc if b+c=3a then $cot invisible function application straight B over 2 times cot invisible function application straight C over 2$ has the value equal to –

In a $capital delta A B C open parentheses fraction numerator a to the power of 2 end exponent over denominator sin invisible function application A end fraction plus fraction numerator b to the power of 2 end exponent over denominator sin invisible function application B end fraction plus fraction numerator c to the power of 2 end exponent over denominator sin invisible function application C end fraction close parentheses times s i n invisible function application fraction numerator A over denominator 2 end fraction s i n invisible function application fraction numerator B over denominator 2 end fraction s i n invisible function application fraction numerator C over denominator 2 end fraction$ simplifies to

In a $capital delta A B C open parentheses fraction numerator a to the power of 2 end exponent over denominator sin invisible function application A end fraction plus fraction numerator b to the power of 2 end exponent over denominator sin invisible function application B end fraction plus fraction numerator c to the power of 2 end exponent over denominator sin invisible function application C end fraction close parentheses times s i n invisible function application fraction numerator A over denominator 2 end fraction s i n invisible function application fraction numerator B over denominator 2 end fraction s i n invisible function application fraction numerator C over denominator 2 end fraction$ simplifies to

parallel

In a triangle ABC, a: b: c = 4: 5: 6. Then 3A + B equals to :

In a triangle ABC, a: b: c = 4: 5: 6. Then 3A + B equals to :

A bullet of mass $m$ is fired with a velocity of 50 $m s to the power of negative 1 end exponent$ at an angle $theta$ with the horizontal. At the highest point of its trajectory, it collides had on with a bob of massless string of length $l equals 10 divided by 3$ m and gets embedded in the bob. After the collision, the string moves to an angle of 120 $degree$ . What is the angle $theta ?$

A bullet of mass $m$ is fired with a velocity of 50 $m s to the power of negative 1 end exponent$ at an angle $theta$ with the horizontal. At the highest point of its trajectory, it collides had on with a bob of massless string of length $l equals 10 divided by 3$ m and gets embedded in the bob. After the collision, the string moves to an angle of 120 $degree$ . What is the angle $theta ?$

physics-General

A spherical hollow is made in a lead sphere of radius $R$ such that its surface touches the outside surface of lead sphere and passes through the centre. What is the shift in the centre of lead sphere as a result of this hollowing?

A spherical hollow is made in a lead sphere of radius $R$ such that its surface touches the outside surface of lead sphere and passes through the centre. What is the shift in the centre of lead sphere as a result of this hollowing?

physics-General

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.