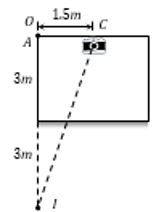
Figure shows a cubical room ABCD with the wall CD as a plane mirror. Each side of the room is 3m. We place a camera at the midpoint of the wall AB. At what distance should the camera be focussed to photograph an object placed at A

Two point white dots are 1mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm. Approximately, what is the maximum distance at which dots can be resolved by the eye ? [Take wavelength of light = 500 nm]

We can only apply the L’Hospital’s rule if the direct substitution returns an indeterminate form, that means 

We can only apply the L’Hospital’s rule if the direct substitution returns an indeterminate form, that means 

We can only apply the L’Hospital’s rule if the direct substitution returns an indeterminate form, that means 

A container is filled with water ( = 1.33) upto a height of 33.25 cm. A concave mirror is placed 15 cm above the water level and the image of an object placed at the bottom is formed 25 cm below the water level. The focal length of the mirror is

light source is located at as shown in the figure. All sides of the polygon are equal. The intensity of illumination at is . What will be the intensity of illumination at

A container of volume 1m³ is divided into two equal compartments, one of which contains an ideal gas at 300 K The other compartment is vacuum The whole system is thermally isolated from its surroundings The partition is removed and the gas expands to occupy the whole volume of the container Its temperature now would be

Two moles of an ideal monoatomic gas at occupies a volume of V If the gas is expanded adiabatically to the volume 2V, then the work done by the gas will be

One mole of an ideal gas undergoes an isothermal change at temperature 'T' so that its volume V is doubled R is the molar gas constant Work done by the gas during this change is

We can only apply the L’Hospital’s rule if the direct substitution returns an indeterminate form, that means 

If then xy+1=

A wire of length 2 m is made from 10 cm³ of copper. A force F is applied so that its length increases by 2 mm. Another wire of length 8 m is made from the same volume of copper. If the force F is applied to it, its length will increase by….