Physics-
General
Easy
Question
Three identical plane mirrors AB, BC, AC are arranged as shown in the figure. Find the total number of images of a point object ' S ' formed by the three mirrors. ( S is at the centre of the system)
- 18
- 12
- 5
- 15
The correct answer is: 12
Related Questions to study
physics-
A transparent solid sphere of radius 2 cm and density 
floats in a transparent liquid of density 
kept in a beaker. The bottom of the beaker is spherical in shape with its radius of anvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an abject is placed at a distance of 10 cm directly above the centre of the sphere its final image coincide with it. If ' h ' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is 
and that of the liquid is 
.
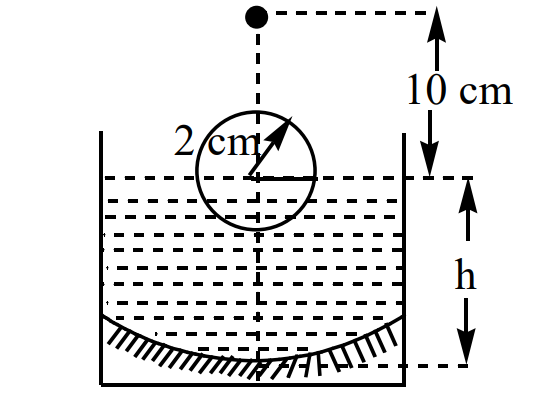
The value of 
is (nearly equal to)
A transparent solid sphere of radius 2 cm and density floats in a transparent liquid of density kept in a beaker. The bottom of the beaker is spherical in shape with its radius of anvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an abject is placed at a distance of 10 cm directly above the centre of the sphere its final image coincide with it. If ' h ' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is and that of the liquid is .
The value of is (nearly equal to)
physics-General
physics-
A transparent solid sphere of radius 2 cm and density floats in a transparent liquid of density kept in a beaker. The bottom of the beaker is spherical in shape with its radius of anvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an abject is placed at a distance of 10 cm directly above the centre of the sphere its final image coincide with it. If ' h ' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is and that of the liquid is .
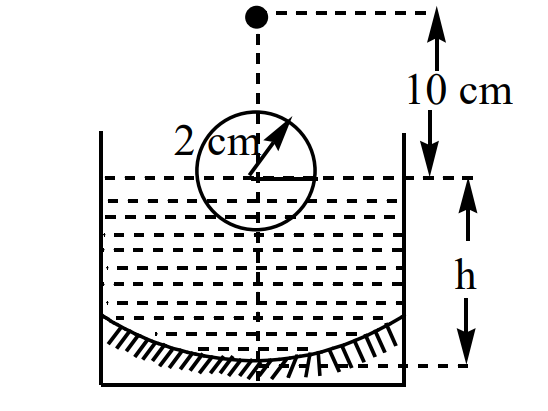
The image formed by the top spherical portion of sphere is (as measured from top of spherical ball)
A transparent solid sphere of radius 2 cm and density floats in a transparent liquid of density kept in a beaker. The bottom of the beaker is spherical in shape with its radius of anvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an abject is placed at a distance of 10 cm directly above the centre of the sphere its final image coincide with it. If ' h ' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is and that of the liquid is .
The image formed by the top spherical portion of sphere is (as measured from top of spherical ball)
physics-General
physics-
A ray of light is incident normally on one face of 
prism of refractive index 5/3 immersed in water of refractive index 
as shown in figure.
A ray of light is incident normally on one face of prism of refractive index 5/3 immersed in water of refractive index as shown in figure.
physics-General
physics-
Two identical thin isosceles prisms of prism angle each A and refractive index 
are placed with their bases touching each other. This system acts as a converging lens. What is the focal length of this system for parallel rays at a distance h from the base of the prism ?
Two identical thin isosceles prisms of prism angle each A and refractive index are placed with their bases touching each other. This system acts as a converging lens. What is the focal length of this system for parallel rays at a distance h from the base of the prism ?
physics-General
physics-
In the given figure, there are two thin lenses of same focal length 
arranged with their principal axes inclined at angle 
. The separation between the optical centers of the lenses is 2f. A point object lies on the principal axis of the convex lens at a large distance to the left of the convex lens. Find the co-ordinates of the final image formed by the system of lenses taking 'O' as the origin of co-ordinate axes.
In the given figure, there are two thin lenses of same focal length arranged with their principal axes inclined at angle . The separation between the optical centers of the lenses is 2f. A point object lies on the principal axis of the convex lens at a large distance to the left of the convex lens. Find the co-ordinates of the final image formed by the system of lenses taking 'O' as the origin of co-ordinate axes.
physics-General
physics-
An equiconvex lens 
of focal length 20 cm is cut into two equal parts and one part 
is silvered. Another concavo-convex lens 
(radii 10 cm and 20 cm, μ=1.5 ) is placed with its principle axis 2 mm above the principle axis of 
A point object ' O ' is placed at a distance of 80 cm from the lens on its principal axis as shown in figure. Find the position of final image.
An equiconvex lens of focal length 20 cm is cut into two equal parts and one part is silvered. Another concavo-convex lens (radii 10 cm and 20 cm, μ=1.5 ) is placed with its principle axis 2 mm above the principle axis of A point object ' O ' is placed at a distance of 80 cm from the lens on its principal axis as shown in figure. Find the position of final image.
physics-General
physics-
A point object 'O' is placed at a distance of 30 cm from a convex lens ( f=20 cm ) cut into two equal haves each of which is displaced by 0.05 cm as shown in figure. Find the position of image? If more than one image is formed, find their number and distance between them.
A point object 'O' is placed at a distance of 30 cm from a convex lens ( f=20 cm ) cut into two equal haves each of which is displaced by 0.05 cm as shown in figure. Find the position of image? If more than one image is formed, find their number and distance between them.
physics-General
physics-
Figure shows an arrangement of an equiconvex lens ( f=20 cm in air) and a concave mirror (R=80 cm). A point object ' O ' is placed on the principal axis at a distance 40 cm from the lens such that the final image is also formed at the position of object. Find d.
Figure shows an arrangement of an equiconvex lens ( f=20 cm in air) and a concave mirror (R=80 cm). A point object ' O ' is placed on the principal axis at a distance 40 cm from the lens such that the final image is also formed at the position of object. Find d.
physics-General
physics-
A thin biconvex lens of refractive index 
is placed an a horizontal plane mirror as shown in mirror. The space between the lens and the mirror is filled with water of refractive index . It is found that when a point object is placed 
above the lens on its principal axis, the object coincides with its Onn image. On repeating with another liquid, the object and the image again coincide at a distance of 
from the lens. Calculate refractive index of the liquid.
A thin biconvex lens of refractive index is placed an a horizontal plane mirror as shown in mirror. The space between the lens and the mirror is filled with water of refractive index . It is found that when a point object is placed above the lens on its principal axis, the object coincides with its Onn image. On repeating with another liquid, the object and the image again coincide at a distance of from the lens. Calculate refractive index of the liquid.
physics-General
physics-
An object is placed at a distance of 
from a thin plano convex lens of focal length . The plane surface of lens is now silvered. What is the position of image?
An object is placed at a distance of from a thin plano convex lens of focal length . The plane surface of lens is now silvered. What is the position of image?
physics-General
physics-
A glass slab of thickness 3 cm and refractive index 1.5 is placed 12 cm from concave lens of focal length 20 cm. A convex lens of focal length 10 cm is placed on the same axis at a distance of 5 cm from the concave lens. An object is located 6 cm in front of glass slab and an observer looks it from the other end of optical train. Where will the object appear to be? What is the magnification of the object?
A glass slab of thickness 3 cm and refractive index 1.5 is placed 12 cm from concave lens of focal length 20 cm. A convex lens of focal length 10 cm is placed on the same axis at a distance of 5 cm from the concave lens. An object is located 6 cm in front of glass slab and an observer looks it from the other end of optical train. Where will the object appear to be? What is the magnification of the object?
physics-General
physics-
A converging lens of focal length 20 cm is separated by 8 cm from a diverging lens of focal length 30 cm. A parallel beam of light falls on after passing through is focused at point 
. Calculate V. Repeat the calculation for the case when the parallel beam first falls on .
A converging lens of focal length 20 cm is separated by 8 cm from a diverging lens of focal length 30 cm. A parallel beam of light falls on after passing through is focused at point . Calculate V. Repeat the calculation for the case when the parallel beam first falls on .
physics-General
physics-
A thin plano convex lens is split into two halves. One of the haves is shifted along the optical axis. The separation between object and image planes is 1.8 m. The magnification of the image formed by one half of lens is 2. Find the focal length of the lens and separation between the halves.
A thin plano convex lens is split into two halves. One of the haves is shifted along the optical axis. The separation between object and image planes is 1.8 m. The magnification of the image formed by one half of lens is 2. Find the focal length of the lens and separation between the halves.
physics-General
physics-
A point object 'O' approaches a biconvex lens of focal length 40 cm along its optic axis with a speed of 
while the later recedes away from the former with a speed of 4 cm/s. Find the speed and direction of motion of the image when the abject is at a distance of 60 cm from the lens.
A point object 'O' approaches a biconvex lens of focal length 40 cm along its optic axis with a speed of while the later recedes away from the former with a speed of 4 cm/s. Find the speed and direction of motion of the image when the abject is at a distance of 60 cm from the lens.
physics-General
physics-
A convex lens of focal length 24 cm in air is surrounded by different mediums as shown in the fig. A point object 0 is placed along the principle axis at a distance 30 cm from the lens. Find the number and position of the images formed.
A convex lens of focal length 24 cm in air is surrounded by different mediums as shown in the fig. A point object 0 is placed along the principle axis at a distance 30 cm from the lens. Find the number and position of the images formed.
physics-General
