Question
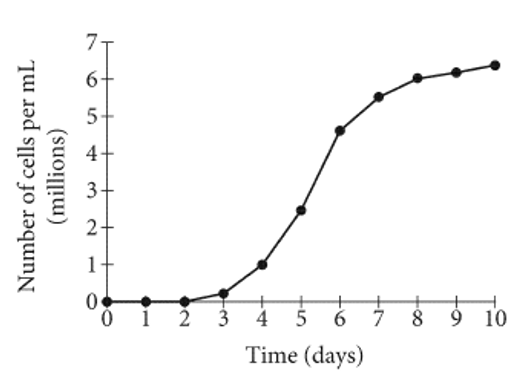
The graph shows the number of algae cells grown during an experiment, in millions of cells per milliliter (mL) of water, d days after the start of an experiment. Between which two days was the growth rate, in millions of cells per  of water per day, of the algae the greatest?
of water per day, of the algae the greatest?
- Day 4 and day 5
- Day 5 and day 6
- Day 7 and day 8
- Day 9 and day 10
The correct answer is: Day 5 and day 6
HINT: Observe the graph and thus we will get the greatest growth.
Complete step by step Solution
It is clear from the graph that the greatest jump is between day 5 and day 6.
So it is between day 5 and day 6 that the growth rate, in millions of cells per mL of water per day, of the algae is the greatest.
Hence option B is the correct answer.
Related Questions to study
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.
The function  is defined by
is defined by  . What is the value of f(3) ?
. What is the value of f(3) ?
The function  is defined by
is defined by  . What is the value of f(3) ?
. What is the value of f(3) ?
The combustion of glucose releases energy. The ratio of grams of glucose combusted to kilocalories of energy released is 12.0 to 45.0. How many grams of glucose must be combusted to provide 85.5 kilocalories of energy?
The combustion of glucose releases energy. The ratio of grams of glucose combusted to kilocalories of energy released is 12.0 to 45.0. How many grams of glucose must be combusted to provide 85.5 kilocalories of energy?
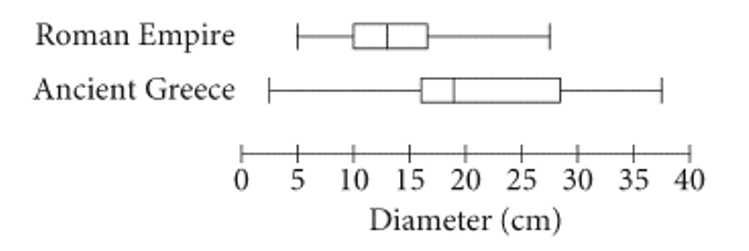
The Metropolitan Museum of Art has plates on display from the Roman Empire and ancient Greece. The box plots shown summarize the distributions of the diameters, in centimeters, of all the museum's plates from each region. How does the median diameter of the plates from the Roman Empire, r, compare to the median diameter of the plates from ancient Greece, g ?

The Metropolitan Museum of Art has plates on display from the Roman Empire and ancient Greece. The box plots shown summarize the distributions of the diameters, in centimeters, of all the museum's plates from each region. How does the median diameter of the plates from the Roman Empire, r, compare to the median diameter of the plates from ancient Greece, g ?
In 2015 , the city of Miami had a population of 441,000 people and an area of 36 square miles. What was the population density of Miami, in people per square mile, in 2015?
In 2015 , the city of Miami had a population of 441,000 people and an area of 36 square miles. What was the population density of Miami, in people per square mile, in 2015?
A sample of water was taken from each of ten different locations in a pond. The pH of each sample was measured. The measurements are summarized in the frequency table shown.
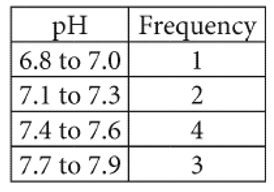
How many samples have a pH of 7.4 or greater?
A sample of water was taken from each of ten different locations in a pond. The pH of each sample was measured. The measurements are summarized in the frequency table shown.

How many samples have a pH of 7.4 or greater?
The function  models the number of water hyacinths in a population over time, where A(t) is the number of water hyacinths and
models the number of water hyacinths in a population over time, where A(t) is the number of water hyacinths and  is the time, in days since the population was measured. Which is the best interpretation of
is the time, in days since the population was measured. Which is the best interpretation of  in this context?
in this context?
The function  models the number of water hyacinths in a population over time, where A(t) is the number of water hyacinths and
models the number of water hyacinths in a population over time, where A(t) is the number of water hyacinths and  is the time, in days since the population was measured. Which is the best interpretation of
is the time, in days since the population was measured. Which is the best interpretation of  in this context?
in this context?
The graph of the function f is shown. Which of the following is the value of x for which f(x) = 0 ?

The graph of the function f is shown. Which of the following is the value of x for which f(x) = 0 ?

What is the graph of the equation  ?
?
What is the graph of the equation  ?
?
Two beach balls are each in the shape of a sphere. The larger beach ball has a diameter of 3x, and the smaller beach ball has a diameter of x. What is the ratio of the volume of the larger beach ball to volume of the smaller beach ball?
volume of a sphere
A sphere is a collection of points in space separated by r from the center. The quantity of space a solid in three dimensions takes up is known as its volume. The unit of volume is measured in cubic (in3, ft3, cm3, m3, et cetera). Before calculating the volume, ensure all measurements are in the same unit.
Follow the steps below to determine the volume of a given sphere:
Step 1: Compare the radius of the given sphere. If you know the diameter of the sphere, divide it by two to get the radius.
Step 2: Find the radius of r'³s cube.
Step 3: Now divide it by (4/3) π
Step 4: The volume of the sphere will be the final answer.
The volume V of a sphere is equal to four-thirds of pi times the cube of the radius.
V = 4/3πr³
A hemisphere's volume is equal to one-half that of its related sphere.
Two beach balls are each in the shape of a sphere. The larger beach ball has a diameter of 3x, and the smaller beach ball has a diameter of x. What is the ratio of the volume of the larger beach ball to volume of the smaller beach ball?
volume of a sphere
A sphere is a collection of points in space separated by r from the center. The quantity of space a solid in three dimensions takes up is known as its volume. The unit of volume is measured in cubic (in3, ft3, cm3, m3, et cetera). Before calculating the volume, ensure all measurements are in the same unit.
Follow the steps below to determine the volume of a given sphere:
Step 1: Compare the radius of the given sphere. If you know the diameter of the sphere, divide it by two to get the radius.
Step 2: Find the radius of r'³s cube.
Step 3: Now divide it by (4/3) π
Step 4: The volume of the sphere will be the final answer.
The volume V of a sphere is equal to four-thirds of pi times the cube of the radius.
V = 4/3πr³
A hemisphere's volume is equal to one-half that of its related sphere.



