Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

Assertion : The side of regular hexagon is 5 cm whose radius of inscribed circle is 5cm.
Reason : The radius of inscribed circle of a regular polygon of side a is $fraction numerator a over denominator 2 end fraction cot invisible function application open parentheses fraction numerator pi over denominator n end fraction close parentheses$ .

If both (A) and (R) are true, and (R) is the correct explanation of (A).
If both (A) and (R) are true but (R) is not the correct explanation of (A).
If (A) is true but (R) is false.
If (A) is false but (R) is true.

The correct answer is: If (A) is false but (R) is true.

Related Questions to study

Assertion : In a ABC, $fraction numerator a cos invisible function application A plus b cos invisible function application B plus c cos invisible function application C over denominator a plus b plus c end fraction$ is equal to $fraction numerator r over denominator R end fraction$
Reason : In equilateral triangle the ratio between In-radius and circum-radius is 1 : 2.

Assertion : In a ABC, $fraction numerator a cos invisible function application A plus b cos invisible function application B plus c cos invisible function application C over denominator a plus b plus c end fraction$ is equal to $fraction numerator r over denominator R end fraction$
Reason : In equilateral triangle the ratio between In-radius and circum-radius is 1 : 2.

Assertion : In any triangle ABC, $fraction numerator 1 over denominator a b end fraction plus fraction numerator 1 over denominator b c end fraction plus fraction numerator 1 over denominator c a end fraction equals fraction numerator 1 over denominator 2 r R end fraction$ , where r is in radius and R is circum radius.
Reason : R  2r.

Assertion : In any triangle ABC, $fraction numerator 1 over denominator a b end fraction plus fraction numerator 1 over denominator b c end fraction plus fraction numerator 1 over denominator c a end fraction equals fraction numerator 1 over denominator 2 r R end fraction$ , where r is in radius and R is circum radius.
Reason : R  2r.

In any equilateral , three circles of radii one are touching to the sides given as in the figure then area of the 

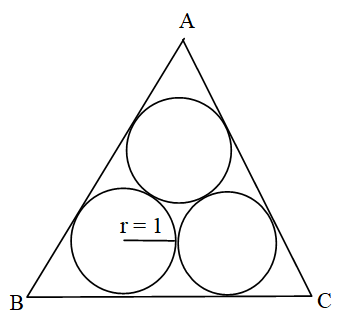
In any equilateral , three circles of radii one are touching to the sides given as in the figure then area of the 
Maths-General

parallel

If the sides a, b, c of a triangle are such that a : b : c : : 1 : $square root of 3$ : 2, then the A : B : C is -

If the sides a, b, c of a triangle are such that a : b : c : : 1 : $square root of 3$ : 2, then the A : B : C is -

If the angles of a triangle are in ratio 4 : 1: 1 then the ratio of the longest side and perimeter of triangle is -

If the angles of a triangle are in ratio 4 : 1: 1 then the ratio of the longest side and perimeter of triangle is -

Which of the following pieces of data does NOT uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle) -

Which of the following pieces of data does NOT uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle) -

parallel

In a triangle ABC, let C = $fraction numerator pi over denominator 2 end fraction$ . If r is the in radius and R is the circumradius of the triangle, then 2(r + R) is equal to -

In a triangle ABC, let C = $fraction numerator pi over denominator 2 end fraction$ . If r is the in radius and R is the circumradius of the triangle, then 2(r + R) is equal to -

The solution set of the equation $fraction numerator 1 over denominator left parenthesis x plus 3 right parenthesis end fraction less or equal than negative 2 space i s$

The solution set of the equation $fraction numerator 1 over denominator left parenthesis x plus 3 right parenthesis end fraction less or equal than negative 2 space i s$

Solution of $left parenthesis 5 x minus 1 right parenthesis less than left parenthesis x plus 1 right parenthesis squared less than left parenthesis 7 x minus 3 right parenthesis$ is

Solution of $left parenthesis 5 x minus 1 right parenthesis less than left parenthesis x plus 1 right parenthesis squared less than left parenthesis 7 x minus 3 right parenthesis$ is

parallel

Let A0 A1 A2 A3 A4 A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0A2 , and A0A4 is -

Let A0 A1 A2 A3 A4 A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0A2 , and A0A4 is -

Let L sin  = 10 + log sin . The number of triangles ABC such that log b + 10 = log c + L sin B is-

Let L sin  = 10 + log sin . The number of triangles ABC such that log b + 10 = log c + L sin B is-

If for a ABC, cot A. cot B. cot C > 0 then the triangle is-

If for a ABC, cot A. cot B. cot C > 0 then the triangle is-

parallel

In a triangle PQR as shown in figure given that x : y : z :: 2 : 3 : 6, then the value of QPR is -

In a triangle PQR as shown in figure given that x : y : z :: 2 : 3 : 6, then the value of QPR is -
Maths-General

The in-radius of the triangle formed by the axes and the line 4x + 3y – 12 = 0 is -

The in-radius of the triangle formed by the axes and the line 4x + 3y – 12 = 0 is -

In a  ABC if r1 = 2r2 = 3r3, then -

In a  ABC if r1 = 2r2 = 3r3, then -

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.