Question
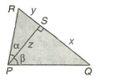
If  where a<1, b<1 then
where a<1, b<1 then
- xy+xz=yz+x
- xyz=x+y+z
- xy+yz=xz+y
- yz+zx=xy+z

We can write x as

Similarly, we can write y as

Similarly, we can write z as

Multiply ab and equate the values and simplify
The correct answer is: yz+zx=xy+z
Given :  , where a<1, b<1
, where a<1, b<1
To find : A relationship between x, y and z
We can write x as

Similarly, we can write y as

Similarly, we can write z as


Solving the above, we get

Related Questions to study
If l, m, n are the  terms of a G.P which are +ve, then
terms of a G.P which are +ve, then 
If l, m, n are the  terms of a G.P which are +ve, then
terms of a G.P which are +ve, then 
The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm

The relationship between force and position is shown in the figure given (in one dimensional case) calculate the work done by the force in displacing a body from x=0 cm to x=5 cm

Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.
Fifth term of G.P is 2 The product of its first nine terms is
Here note that the fifth term is having fourth power of 2 and not fifth power. We need not to find all nine terms separately; only finding the product is enough because that product will then be written in the form of the term that is known. Terms in a G.P. are having a common ratio in between. That’s why the power of r is increasing as the terms are increasing.