Maths-
General
Easy
Question
The point on the ellipse 16x2 + 9y2 = 400 where ordinate decrease at the same rate at which the abscissa increases is
- (9, 16)




We are given the equation of ellipse. We are given that the rate of decrease of ordinante is same as the rate of increase of abscissa. Rate means change w.r.t the time. To find the rate of change of quantity, we take it's derivative w.r.t time. We have to find the point at which the rate is as given above.
The correct answer is: 
The given equation of ellipse is 16x2 + 9y2 = 400
Ordinate means distance of the point from x-axis. It is given by y coordinate.
Abscissa means distance of the point from the y-axis. It is given by x coordinate.
We are given that, .....(1)
.....(1)
We will take the derivate of the equation of ellipse w.r.t time.

Now, to find the points we will substitute the value of x in the equation of ellipse.

Taking square roots of both sides we get,


So, the points satisfying the given condition are 
This is the only point that matches the option  .
.
.
For such questions, we should know how to find the derivates. We should know the concept of abscissa and ordinate.
Related Questions to study
Maths-
The displacement of a particle in time ‘t’ is given by S = t3 – t2 – 8t – 18. The acceleration of the particle when its velocity vanishes is
For such questions, we should know relation between displacement, velocity and time. We should also know how to find first and second order derivate.
The displacement of a particle in time ‘t’ is given by S = t3 – t2 – 8t – 18. The acceleration of the particle when its velocity vanishes is
Maths-General
For such questions, we should know relation between displacement, velocity and time. We should also know how to find first and second order derivate.
Maths-
If  and
and  then
then  is equal to
is equal to
If  and
and  then
then  is equal to
is equal to
Maths-General
Maths-
Maths-General
Maths-
Maths-General
Physics-
The figure shows a transparent slab of length 1 m placed in air whose refractive index in x direction varies as  . The optical path length of ray R will be
. The optical path length of ray R will be

The figure shows a transparent slab of length 1 m placed in air whose refractive index in x direction varies as  . The optical path length of ray R will be
. The optical path length of ray R will be

Physics-General
Physics-
A parallel beam of light 500 nm is incident at an angle 30° with the normal to the slit plane in a young's double slit experiment. The intensity due to each slit is Io. Point O is equidistant from  and
and  . The distance between slits is 1 mm.
. The distance between slits is 1 mm.

A parallel beam of light 500 nm is incident at an angle 30° with the normal to the slit plane in a young's double slit experiment. The intensity due to each slit is Io. Point O is equidistant from  and
and  . The distance between slits is 1 mm.
. The distance between slits is 1 mm.

Physics-General
Physics-
In a Young's Double slit experiment, first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (centre of the screen)

In a Young's Double slit experiment, first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (centre of the screen)

Physics-General
Physics-
An YDSE is carried out in a liquid of refractive index  and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. The wavelength of light in air is
and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. The wavelength of light in air is  and D/d=1000.
and D/d=1000.

An YDSE is carried out in a liquid of refractive index  and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. The wavelength of light in air is
and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. The wavelength of light in air is  and D/d=1000.
and D/d=1000.

Physics-General
Physics-
Two coherent radio point sources that are separated by 2.0 m are radiating in phase with a wavelength of 0.25 m. If a detector moves in a large circle around their midpoint, at how many points will the detector show a maximum signal ?
Two coherent radio point sources that are separated by 2.0 m are radiating in phase with a wavelength of 0.25 m. If a detector moves in a large circle around their midpoint, at how many points will the detector show a maximum signal ?
Physics-General
Physics-
Two coherent narrow slits emitting light of wavelength  in the same phase are placed parallel to each other at a small separation of
in the same phase are placed parallel to each other at a small separation of  . The light is collected on a screen S which is placed at a distance
. The light is collected on a screen S which is placed at a distance  from the slit
from the slit  as shown in figure. Find the finite distance x such that the intensity of P is equal to intensity at O.
as shown in figure. Find the finite distance x such that the intensity of P is equal to intensity at O.

Two coherent narrow slits emitting light of wavelength  in the same phase are placed parallel to each other at a small separation of
in the same phase are placed parallel to each other at a small separation of  . The light is collected on a screen S which is placed at a distance
. The light is collected on a screen S which is placed at a distance  from the slit
from the slit  as shown in figure. Find the finite distance x such that the intensity of P is equal to intensity at O.
as shown in figure. Find the finite distance x such that the intensity of P is equal to intensity at O.

Physics-General
Physics-
Consider the arrangement shown in figure. By some mechanism, the separation between the slits  and
and  can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of
can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of  and
and  . When
. When  , the intensity measured at P is I. Find this intensity when z is equal to
, the intensity measured at P is I. Find this intensity when z is equal to
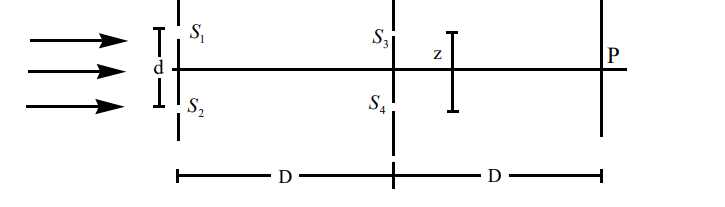
1)  ,
,
2)  , and
, and
3)  .
.
Consider the arrangement shown in figure. By some mechanism, the separation between the slits  and
and  can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of
can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of  and
and  . When
. When  , the intensity measured at P is I. Find this intensity when z is equal to
, the intensity measured at P is I. Find this intensity when z is equal to

1)  ,
,
2)  , and
, and
3)  .
.
Physics-General
Maths-
Maths-General
Physics-
In Young's double slit experiment  and
and  are two slits. Films of thicknesses
are two slits. Films of thicknesses  and
and  and refractive indices
and refractive indices  and
and  are placed in front of
are placed in front of  and
and  respectively. If
respectively. If  , then the central maximum will :
, then the central maximum will :

In Young's double slit experiment  and
and  are two slits. Films of thicknesses
are two slits. Films of thicknesses  and
and  and refractive indices
and refractive indices  and
and  are placed in front of
are placed in front of  and
and  respectively. If
respectively. If  , then the central maximum will :
, then the central maximum will :

Physics-General
Physics-
Two coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. The wavelength of monochromatic light used if it produces the second dark fringes at a distance of 10 mm
Two coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. The wavelength of monochromatic light used if it produces the second dark fringes at a distance of 10 mm
Physics-General
Physics-
Two coherent monochromatic light beams of intensities I and 4I are superposed. The maximum and minimum possible intensities in the resulting beam are
Two coherent monochromatic light beams of intensities I and 4I are superposed. The maximum and minimum possible intensities in the resulting beam are
Physics-General





