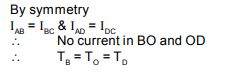Physics-
General
Easy
Question
All the rods have same conductance ‘K’ and same area of cross section ‘A’. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct:
- Rate of heat flow through ABC, AOC and ADC is same
- Rate of heat flow through BO and OD is not same
- Total Rate of heat flow from A to C is
- Temperature at junctions B, O and D are same
The correct answer is: Rate of heat flow through BO and OD is not same
Related Questions to study
Physics-
Two large non conducting plates having surface charge densities + s and –s respectively, are fixed d distance apart. A small test charge q of mass m is attached to two non conducting springs each of spring constant k as shown in the figure. The sum of lengths of both springs in undeformed state is d. The charge q is released from rest with both the springs nondeformed. Then charge q will (neglect gravity)
Two large non conducting plates having surface charge densities + s and –s respectively, are fixed d distance apart. A small test charge q of mass m is attached to two non conducting springs each of spring constant k as shown in the figure. The sum of lengths of both springs in undeformed state is d. The charge q is released from rest with both the springs nondeformed. Then charge q will (neglect gravity)
Physics-General
Physics-
As shown in the figure a variable force F is applied on conducting wire of length l such that its velocity remains constant. There is no resistance in any branch in the circuit. Consider the motion of wire from t = 0 initially there is no current in inductor. Now when wire has covered a distance x (from initial position) then at that time energy of inductor will be: (Neglect gravity)
As shown in the figure a variable force F is applied on conducting wire of length l such that its velocity remains constant. There is no resistance in any branch in the circuit. Consider the motion of wire from t = 0 initially there is no current in inductor. Now when wire has covered a distance x (from initial position) then at that time energy of inductor will be: (Neglect gravity)
Physics-General
Physics-
The state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is 
then the pressure of the gas in state C is :
The state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is then the pressure of the gas in state C is :
Physics-General
Physics-
P-T diagram is shown below then choose the corresponding V-T diagram
P-T diagram is shown below then choose the corresponding V-T diagram
Physics-General
Physics-
A fixed container is fitted with a piston which is attached to a spring of spring constant k. The other end of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an ideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotational kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
A fixed container is fitted with a piston which is attached to a spring of spring constant k. The other end of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an ideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotational kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
Physics-General
Physics-
The side of the cube is 'l' and point charges are kept at each corner as shown in diagram. Interaction electrostatic potential energy of all the charges is :
The side of the cube is 'l' and point charges are kept at each corner as shown in diagram. Interaction electrostatic potential energy of all the charges is :
Physics-General
Physics-
For a given thermodynamic cyclic process, P – V indicator diagram is as shown in the figure. Process AB, BC & CA are isobaric, adiabatic & isothermal respectively. Then which of the following curve represent correct V – T indicator diagram for the process ABCA?
For a given thermodynamic cyclic process, P – V indicator diagram is as shown in the figure. Process AB, BC & CA are isobaric, adiabatic & isothermal respectively. Then which of the following curve represent correct V – T indicator diagram for the process ABCA?
Physics-General
Physics-
One mole of an ideal gas is kept enclosed under a light piston (area=10– 2 m2 ) connected by a compressed spring (spring constant 100 N/m). The volume of gas is 0.83 m3 and its temperature is 100K. The gas is heated slowly so that it compresses the spring further by 0.1 m. The work done by the gas in the process is: (Take R = 8.3 J/K-mole and suppose there is no atmosphere).
One mole of an ideal gas is kept enclosed under a light piston (area=10– 2 m2 ) connected by a compressed spring (spring constant 100 N/m). The volume of gas is 0.83 m3 and its temperature is 100K. The gas is heated slowly so that it compresses the spring further by 0.1 m. The work done by the gas in the process is: (Take R = 8.3 J/K-mole and suppose there is no atmosphere).
Physics-General
Physics-
A rod of length l is sliding such that one of its ends is always in contact with a vertical wall and its other end is always in contact with horizontal surface. Just after the rod is released from rest, the magnitude of acceleration of end points of the rod is a and b respectively. The angular acceleration of rod at this instant will be
A rod of length l is sliding such that one of its ends is always in contact with a vertical wall and its other end is always in contact with horizontal surface. Just after the rod is released from rest, the magnitude of acceleration of end points of the rod is a and b respectively. The angular acceleration of rod at this instant will be
Physics-General
Physics-
Two sound waves are superimposed. The resulting pressure variation at a single point at a distance 'x' from the source is graphed below :
The beat frequency of the resulting sound wave is :
Two sound waves are superimposed. The resulting pressure variation at a single point at a distance 'x' from the source is graphed below :
The beat frequency of the resulting sound wave is :
Physics-General
Maths-
If roots of the eduation
are real, then find the minimum value of n –m.
If roots of the eduationare real, then find the minimum value of n –m.
Maths-General
Maths-
For 
if
then 
is equal to
For if then is equal to
Maths-General
Maths-
The term independent of x in expansion of
is
The term independent of x in expansion of is
Maths-General
Maths-
The value of
is
The value ofis
Maths-General
General
Complete the following with an appropriate conjunction.
We could not sleep because it was too hot.
Complete the following with an appropriate conjunction.
We could not sleep because it was too hot.
GeneralGeneral
