Maths-
General
Easy
Question
Let f(x) =
, 0 < x < Π/2. Then the minimum value of f(x) is
- 1
- 2
The correct answer is: 1
Related Questions to study
Chemistry-
Stereoisomers,' . which can be interconverted simply by rotation about- sigma bonds, are conformational isomers' while those, which can be converted only by breaking and remaking of bonds and not simply by rotation, are called configurational isomers. The angle between C-C and C-H bonds on adjacent carbon atoms in any conformation is' called· dihedral· angle.
The cyclic compounds most commonly found in nature containing 'six membered rings can exist in a conformation that is almost Completely free of strain. The most stable conformation of cyclohexane.is chair form, According to Bayer strain theory, the greater deviation from the normal tetrahedral angle;. greater is the angle strain or torsional strain and hence lesser is the stability of the cycloalkane.
Dihedral angle in staggered and eclipsed conformations are:
Stereoisomers,' . which can be interconverted simply by rotation about- sigma bonds, are conformational isomers' while those, which can be converted only by breaking and remaking of bonds and not simply by rotation, are called configurational isomers. The angle between C-C and C-H bonds on adjacent carbon atoms in any conformation is' called· dihedral· angle.
The cyclic compounds most commonly found in nature containing 'six membered rings can exist in a conformation that is almost Completely free of strain. The most stable conformation of cyclohexane.is chair form, According to Bayer strain theory, the greater deviation from the normal tetrahedral angle;. greater is the angle strain or torsional strain and hence lesser is the stability of the cycloalkane.
Dihedral angle in staggered and eclipsed conformations are:
Chemistry-General
Maths-
Minimum value of 
is
Minimum value of is
Maths-General
Maths-
The value of cot 
is
The value of cot is
Maths-General
Chemistry-
The IUPAC name of the compound,
is:
The IUPAC name of the compound,
is:
Chemistry-General
Chemistry-
Consider the following structures and pick up the right statements:
I) 
II) 
III) 
Consider the following structures and pick up the right statements:
I)
II)
III)
Chemistry-General
Maths-
The no. of real solutions of (x,y) where 
are
The no. of real solutions of (x,y) where are
Maths-General
Chemistry-
The molecules
are:
The molecules
are:
Chemistry-General
Chemistry-
(A) The boiling point 6f cis-l,2-dichloroethene is higher than corresponding trans-isomer.
(R) The dipole moment of cis-l,2-dichloroethene is higher than trans-isomers.
(A) The boiling point 6f cis-l,2-dichloroethene is higher than corresponding trans-isomer.
(R) The dipole moment of cis-l,2-dichloroethene is higher than trans-isomers.
Chemistry-General
Chemistry-
(A) Metamers can also be chain or position isomers :
(R) The term tautomerism was introduced to explain the reactivity of a substance . according to two possible structures.
(A) Metamers can also be chain or position isomers :
(R) The term tautomerism was introduced to explain the reactivity of a substance . according to two possible structures.
Chemistry-General
Chemistry-
(A) Following amide exist in two Structural forms:
I)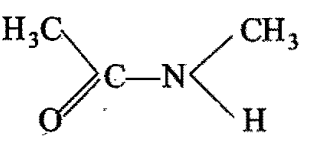 
II) 
(R) Rotation about carbon nitrogen bond is restricted due to resonance.·
(A) Following amide exist in two Structural forms:
I)
II)
(R) Rotation about carbon nitrogen bond is restricted due to resonance.·
Chemistry-General
Maths-
If cosA = cosB + cos3B, sinA = sinB - sin3B. Then |sin(A-B)| =
If cosA = cosB + cos3B, sinA = sinB - sin3B. Then |sin(A-B)| =
Maths-General
Chemistry-
Which of the following is chiral?
Which of the following is chiral?
Chemistry-General
Maths-
statement I: Minimum value of 
is 
statement II: Minimum value of 
is 24 Which of the above statements is correct?
statement I: Minimum value of is
statement II: Minimum value of is 24 Which of the above statements is correct?
Maths-General
Maths-
Maths-General
Maths-
The extreme values of 
over 
are
The extreme values of over are
Maths-General
