Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

If (G,×) is a group such that $left parenthesis a cross times b right parenthesis squared equals left parenthesis a cross times a right parenthesis cross times left parenthesis b cross times b right parenthesis$ for all $a comma b cross times G comma$ then G is

Abelian
Finite
Infinite
None of these

The correct answer is: Abelian

$left parenthesis a cross times b right parenthesis squared equals left parenthesis a cross times a right parenthesis cross times left parenthesis b cross times b right parenthesis text for all end text a comma b element of G$
$rightwards double arrow left parenthesis a cross times b right parenthesis cross times left parenthesis a cross times b right parenthesis equals left parenthesis a cross times a right parenthesis cross times left parenthesis b cross times b right parenthesis text for all end text a comma b element of G$
$rightwards double arrow a cross times left parenthesis b cross times a right parenthesis cross times b equals a cross times left parenthesis a cross times b right parenthesis cross times b text for all end text a comma b element of G$
$rightwards double arrow b cross times a equals a cross times b text for all end text a comma b element of G$
G is abelian.

Related Questions to study

In any group the number of improper subgroups is

In any group the number of improper subgroups is

Shaded region is represented by

Shaded region is represented by

For the following shaded area, the linear constraints except $x greater or equal than 0$ and $y greater or equal than 0$ , are

For the following shaded area, the linear constraints except $x greater or equal than 0$ and $y greater or equal than 0$ , are

parallel

The minimum value of objective function c=2x+2y in the given feasible region, is

The minimum value of objective function c=2x+2y in the given feasible region, is

In a test of Mathematics, there are two types of questions to be answered–short answered and long answered. The relevant data is given below

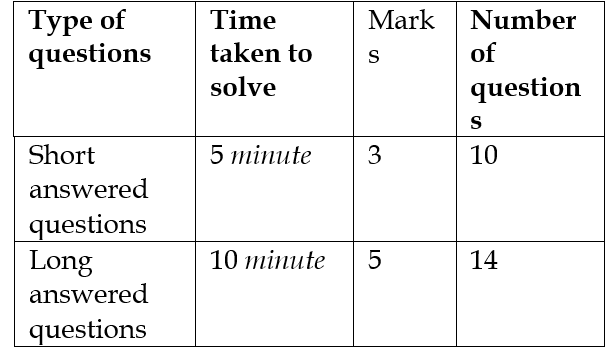
The total marks is 100. Students can solve all the questions. To secure maximum marks, a student solves x short answered and y long answered questions in three hours, then the linear constraints except $x greater or equal than 0 comma y greater or equal than 0$ , are

In a test of Mathematics, there are two types of questions to be answered–short answered and long answered. The relevant data is given below

The total marks is 100. Students can solve all the questions. To secure maximum marks, a student solves x short answered and y long answered questions in three hours, then the linear constraints except $x greater or equal than 0 comma y greater or equal than 0$ , are

The feasible region for the following constraints $L subscript 1 end subscript less or equal than 0 comma L subscript 2 end subscript greater or equal than 0 comma L subscript 3 end subscript equals 0 comma x greater or equal than 0 comma y greater or equal than 0$ in the diagram shown is

The feasible region for the following constraints $L subscript 1 end subscript less or equal than 0 comma L subscript 2 end subscript greater or equal than 0 comma L subscript 3 end subscript equals 0 comma x greater or equal than 0 comma y greater or equal than 0$ in the diagram shown is

parallel

Shaded region is represented by

Shaded region is represented by

For the following feasible region, the linear constraints are

For the following feasible region, the linear constraints are

The maximum value of objective function c=2x+3y in the given feasible region, is

The maximum value of objective function c=2x+3y in the given feasible region, is

parallel

For the following feasible region, the linear constraints except $x greater or equal than 0$ and $y greater or equal than 0$ , are

For the following feasible region, the linear constraints except $x greater or equal than 0$ and $y greater or equal than 0$ , are

For the solution of equation f(x)=0 by the Newton-Raphson method, the value of x tends to root of the equation highly when $f to the power of straight prime open parentheses x subscript n close parentheses$ is

For the solution of equation f(x)=0 by the Newton-Raphson method, the value of x tends to root of the equation highly when $f to the power of straight prime open parentheses x subscript n close parentheses$ is

The formula [where f(x_n–1) and f(x_n)have opposite sign at each step, $n space greater or equal than 1$ ] of method of False Position of successive approximation to find the approximate value of a root of the equation f(x)=0 is

The formula [where f(x_n–1) and f(x_n)have opposite sign at each step, $n space greater or equal than 1$ ] of method of False Position of successive approximation to find the approximate value of a root of the equation f(x)=0 is

parallel

By bisection method, the real root of the equation $x to the power of 3 end exponent minus 9 x plus 1 equals 0$ lying between x=2 and x=4 is nearer to

By bisection method, the real root of the equation $x to the power of 3 end exponent minus 9 x plus 1 equals 0$ lying between x=2 and x=4 is nearer to

A river is 80 feet wide. The depth d (in feet) of the river at a distance of x feet from one bank is given by the following table :

By Simpson’s rule, the area of the cross-section of the river is

A river is 80 feet wide. The depth d (in feet) of the river at a distance of x feet from one bank is given by the following table :

By Simpson’s rule, the area of the cross-section of the river is

If for n=4, the approximate value of integral $not stretchy integral subscript 1 end subscript superscript 9 end superscript x to the power of 2 end exponent d x$ by Trapezoidal rule is $2 open square brackets fraction numerator 1 over denominator 2 end fraction left parenthesis 1 plus 9 to the power of 2 end exponent right parenthesis plus alpha to the power of 2 end exponent plus beta to the power of 2 end exponent plus 7 to the power of 2 end exponent close square brackets$ , then

If for n=4, the approximate value of integral $not stretchy integral subscript 1 end subscript superscript 9 end superscript x to the power of 2 end exponent d x$ by Trapezoidal rule is $2 open square brackets fraction numerator 1 over denominator 2 end fraction left parenthesis 1 plus 9 to the power of 2 end exponent right parenthesis plus alpha to the power of 2 end exponent plus beta to the power of 2 end exponent plus 7 to the power of 2 end exponent close square brackets$ , then

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.