Maths-
General
Easy
Question
Let f : [-10, 10] →R, where f(x) = sin x + 
be an odd function. Then set of values of parameter a is/are
- (-10, 10) – {0}
- (0, 10)
- [100, ¥)
- (100, ¥)
The correct answer is: (100, ¥)
Related Questions to study
physics-
Light wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection the angle of incidence must be greater than
Light wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection the angle of incidence must be greater than
physics-General
maths-
If the function 
f(x) dt → 5 as |x| → I, then the value of ‘a’ so that the equation 2x + f(t) dt = a has at least two roots of opposite signs in (-1, 1) is
If the function f(x) dt → 5 as |x| → I, then the value of ‘a’ so that the equation 2x + f(t) dt = a has at least two roots of opposite signs in (-1, 1) is
maths-General
Maths-
In 
In
Maths-General
chemistry-
On Bohr’s stationary orbits -
On Bohr’s stationary orbits -
chemistry-General
chemistry-
For a valid Bohr orbit, its cicumfrence should be -
For a valid Bohr orbit, its cicumfrence should be -
chemistry-General
chemistry-
Arrange the following particles in increasing order of values of e/m ratio: Electron (e), proton (p), neutron (n) and α-particle (α) -
Arrange the following particles in increasing order of values of e/m ratio: Electron (e), proton (p), neutron (n) and α-particle (α) -
chemistry-General
Maths-
In 
In
Maths-General
physics-
An antenna behaves as resonant circuit only when its length is
An antenna behaves as resonant circuit only when its length is
physics-General
Maths-
If 
If
Maths-General
physics-
In the adjoining diagram, a wavefront AB, moving in air is incident on a plane glass surface XY. Its position CD after refraction through a glass slab is shown also along with the normals drawn at A and D. The refractive index of glass with respect to air (
) will be equal to
In the adjoining diagram, a wavefront AB, moving in air is incident on a plane glass surface XY. Its position CD after refraction through a glass slab is shown also along with the normals drawn at A and D. The refractive index of glass with respect to air () will be equal to
physics-General
chemistry-
Which statement is not correct for n=5,m=2:
Which statement is not correct for n=5,m=2:
chemistry-General
chemistry-
In P-atom find out the no. of paired electrons for l=1 and m =0-
In P-atom find out the no. of paired electrons for l=1 and m =0-
chemistry-General
chemistry-
For H- atom, the energy required for the removal electron from various sub-shells is given at under:
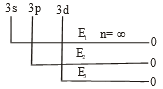The order of the energies would be:
For H- atom, the energy required for the removal electron from various sub-shells is given at under:
The order of the energies would be:
chemistry-General
physics-
Immiscible transparent liquids A, B, C, D and E are placed in a rectangular container of glass with the liquids making layers according to their densities. The refractive index of the liquids are shown in the adjoining diagram. The container is illuminated from the side and a small piece of glass having refractive index 1.61 is gently dropped into the liquid layer. The glass piece as it descends downwards will not be visible in
Immiscible transparent liquids A, B, C, D and E are placed in a rectangular container of glass with the liquids making layers according to their densities. The refractive index of the liquids are shown in the adjoining diagram. The container is illuminated from the side and a small piece of glass having refractive index 1.61 is gently dropped into the liquid layer. The glass piece as it descends downwards will not be visible in
physics-General
Maths-
Values of 
is :
Values of is :
Maths-General
