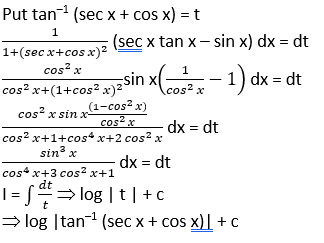Maths-
General
Easy
Question
The indefinite integral of  is, for any arbitrary constant -
is, for any arbitrary constant -
The correct answer is: 
Related Questions to study
maths-
If f  = x + 2 then
= x + 2 then  is equal to
is equal to
If f  = x + 2 then
= x + 2 then  is equal to
is equal to
maths-General
maths-
Let  , then
, then  is equal to:
is equal to:
Let  , then
, then  is equal to:
is equal to:
maths-General
maths-
Statement I : y = f(x) = , x
, x R Range of f(x) is [3/4, 1)
R Range of f(x) is [3/4, 1)
Statement II :  .
.
Statement I : y = f(x) = , x
, x R Range of f(x) is [3/4, 1)
R Range of f(x) is [3/4, 1)
Statement II :  .
.
maths-General
maths-
Statement I : Function f(x) = sinx + {x} is periodic with period 
Statement II : sin x and {x} are both periodic with period  and 1 respectively.
and 1 respectively.
Statement I : Function f(x) = sinx + {x} is periodic with period 
Statement II : sin x and {x} are both periodic with period  and 1 respectively.
and 1 respectively.
maths-General
maths-
Statement 1 : f : R  R and
R and  is bijective.
is bijective.
Statement 2 :  is bijective.
is bijective.
Statement 1 : f : R  R and
R and  is bijective.
is bijective.
Statement 2 :  is bijective.
is bijective.
maths-General
maths-
Statement I : Graph of y = tan x is symmetrical about origin
Statement II : Graph of  is symmetrical about y-axis
is symmetrical about y-axis
Statement I : Graph of y = tan x is symmetrical about origin
Statement II : Graph of  is symmetrical about y-axis
is symmetrical about y-axis
maths-General
maths-
Statement-  If
If  Where
Where  is an identity function.
is an identity function.
Statement-  R defined by
R defined by  is an identity function.
is an identity function.
Statement-  If
If  Where
Where  is an identity function.
is an identity function.
Statement-  R defined by
R defined by  is an identity function.
is an identity function.
maths-General
Maths-
Assertion (A) : 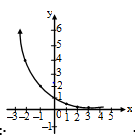 Graph of
Graph of 
Reason (R) : In the expression am/n, where a, m, n × J+, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.
Assertion (A) :  Graph of
Graph of 
Reason (R) : In the expression am/n, where a, m, n × J+, m represents the power to which a is be raised, whereas n determines the root to be taken; these two processes may be administered in either order with the same result.
Maths-General
maths-
Assertion: The period of  is 1/2.
is 1/2.
Reason: The period of x – [x] is 1.
Assertion: The period of  is 1/2.
is 1/2.
Reason: The period of x – [x] is 1.
maths-General
Maths-
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Assertion : Fundamental period of  .
.
Reason : If the period of f(x) is  and the period of g(x) is
and the period of g(x) is  , then the fundamental period of f(x) + g(x) is the L.C.M. of
, then the fundamental period of f(x) + g(x) is the L.C.M. of  and T
and T
Maths-General
Maths-
Assertion: The function defined by  is invertible if and only if
is invertible if and only if  .
.
Reason: A function is invertible if and only if it is one-to-one and onto function.
Assertion: The function defined by  is invertible if and only if
is invertible if and only if  .
.
Reason: A function is invertible if and only if it is one-to-one and onto function.
Maths-General
Maths-
Assertion :  can never become positive.
can never become positive.
Reason : f(x) = sgn x is always a positive function.
Assertion :  can never become positive.
can never become positive.
Reason : f(x) = sgn x is always a positive function.
Maths-General
Maths-
If f (x) = 
If f (x) = 
Maths-General
Maths-
The value of the integral  dx is :
dx is :
The value of the integral  dx is :
dx is :
Maths-General
Maths-
Assertion : Let  be a function defined by f(x) =
be a function defined by f(x) =  . Then f is many-one function.
. Then f is many-one function.
Reason : If either  or
or  domain of f, then y = f(x) is one-one function.</span
domain of f, then y = f(x) is one-one function.</span
Assertion : Let  be a function defined by f(x) =
be a function defined by f(x) =  . Then f is many-one function.
. Then f is many-one function.
Reason : If either  or
or  domain of f, then y = f(x) is one-one function.</span
domain of f, then y = f(x) is one-one function.</span
Maths-General