Question

The table above shows some values of x and their corresponding values of y. Which of the following equations shows a possible relationship between x and y?
- y = x + 2
- y = x - 2
- y = 2x + 3
- y = 3x - 2
The correct answer is: y = x + 2
From the table, we observe the value of y is 2, when x is 0. We need to check the options, in what sequence.
Option A :-
y = x + 2
Substitute x = 0, we get
y = 0 + 2
y = 2 (True)
Option B :-
y = x - 2
Substitute x = 0, we get
y = 0 - 2
y = -2 (False)
Option C :-
y = 2x + 3
Substitute x = 0, we get
y = 2(0) + 3 = 0 + 3
y = 3 (False)
Option D :-
y = 3x - 2
Substitute x = 0, we get
y =3(0) -2 = 0 - 2
y= -2 (False)
Related Questions to study
If  , what is the value of
, what is the value of
If  , what is the value of
, what is the value of
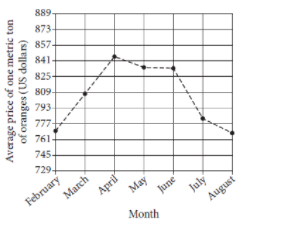
The line graph above shows the average price of one metric ton of oranges, in dollars, for each of seven months in 2014.
Between which two consecutive months shown did the average price of one metric ton of oranges decrease the most?

The line graph above shows the average price of one metric ton of oranges, in dollars, for each of seven months in 2014.
Between which two consecutive months shown did the average price of one metric ton of oranges decrease the most?
Use polynomial identities to factor the polynomials or simplify the expressions : 
Polynomial identities are equations that are true for all possible values of the variable. We can perform polynomial multiplication by applying the distributive property to the multiplication of polynomials.
Use polynomial identities to factor the polynomials or simplify the expressions : 
Polynomial identities are equations that are true for all possible values of the variable. We can perform polynomial multiplication by applying the distributive property to the multiplication of polynomials.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle (using the fourth row).
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle (using the fourth row).
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The expansion of (x + y)n can be also found using the Pascal’s triangle using the (n+1)th row of the triangle.
Use the binomial theorem to expand the expressions: 
The expansion of (x + y)n can be also found using the Pascal’s triangle using the (n+1)th row of the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n, we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n, we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.
Use the binomial theorem to expand the expressions: 
The answer can also be found using the Pascal’s triangle. For the expansion of the expression (x + y)n , we would consider the (n+1)th row in the triangle.



