Question
Which of the following is equivalent to  ?
?
- x
- x + 4


The correct answer is: 
Related Questions to study
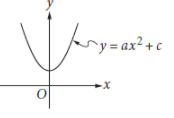
The vertex of the parabola in the xy-plane above is (0, c). Which of the following is true about the
parabola with the equation y = −a(x − b)2 + c ?
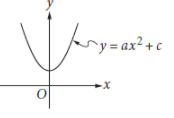
The vertex of the parabola in the xy-plane above is (0, c). Which of the following is true about the
parabola with the equation y = −a(x − b)2 + c ?
Jaime is preparing for a bicycle race. His goal is to bicycle an average of at least 280 miles per week for 4 weeks. He bicycled 240 miles the first week, 310 miles the second week, and 320 miles the third week. Which inequality can be used to
represent the number of miles, x, Jaime could bicycle on the 4th week to meet his goal?
Jaime is preparing for a bicycle race. His goal is to bicycle an average of at least 280 miles per week for 4 weeks. He bicycled 240 miles the first week, 310 miles the second week, and 320 miles the third week. Which inequality can be used to
represent the number of miles, x, Jaime could bicycle on the 4th week to meet his goal?
|
x |
w(x) |
t(x) |
|
1 |
-1 |
-3 |
|
2 |
3 |
-1 |
|
3 |
4 |
1 |
|
4 |
3 |
3 |
|
5 |
-1 |
5 |
|
x |
w(x) |
t(x) |
|
1 |
-1 |
-3 |
|
2 |
3 |
-1 |
|
3 |
4 |
1 |
|
4 |
3 |
3 |
|
5 |
-1 |
5 |
6x − 9y > 12
Which of the following inequalities is equivalent to the inequality above?
Equivalent Inequalities
Equivalent inequalities are defined as inequalities that transmit the same information.
There are several methods for creating equal inequalities.
An inequity is equal to its mirror image, to start with. Let's take a look at what that appears to be:
x > 4
4 < x
Keep in mind that one inequality is effectively the reverse of the other. The inequality symbol's pointed portion always points in the direction of 4! In this situation, the disparities are equal. You must, however, pay VERY close attention to the inequality sign's orientation.
Example 1: The pointed portion of the inequality sign in the first inequality points to 4, whereas the pointy portion in the second inequality points to x, making these two inequality NOT equal:
x > 4
4 < x
6x − 9y > 12
Which of the following inequalities is equivalent to the inequality above?
Equivalent Inequalities
Equivalent inequalities are defined as inequalities that transmit the same information.
There are several methods for creating equal inequalities.
An inequity is equal to its mirror image, to start with. Let's take a look at what that appears to be:
x > 4
4 < x
Keep in mind that one inequality is effectively the reverse of the other. The inequality symbol's pointed portion always points in the direction of 4! In this situation, the disparities are equal. You must, however, pay VERY close attention to the inequality sign's orientation.
Example 1: The pointed portion of the inequality sign in the first inequality points to 4, whereas the pointy portion in the second inequality points to x, making these two inequality NOT equal:
x > 4
4 < x
A motor powers a model car so that after starting from rest, the car travels s inches in t seconds, where s = 16t  . Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
. Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
A motor powers a model car so that after starting from rest, the car travels s inches in t seconds, where s = 16t  . Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
. Which of the following gives the average speed of the car, in inches per second, over the first t seconds after it starts?
Two different points on a number line are both 3 units from the point with coordinate −4. The solution to which of the following equations gives the coordinates of both points?
Two different points on a number line are both 3 units from the point with coordinate −4. The solution to which of the following equations gives the coordinates of both points?
In the xy-plane, the graph of 2x2 − 6x + 2y2 + 2y = 45 is a circle. What is the radius of the circle?
In the xy-plane, the graph of 2x2 − 6x + 2y2 + 2y = 45 is a circle. What is the radius of the circle?
A gear ratio r: s is the ratio of the number of teeth of two connected gears. The ratio of the number of revolutions per minute (rpm) of two gear wheels is s: r. In the diagram below, Gear A is turned by a motor. The turning of Gear A causes Gears B and C to turn as well.
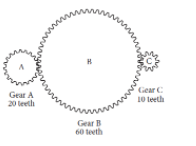
If Gear A is rotated by the motor at a rate of 100 rpm, what is the number of revolutions per minute for Gear C?
A gear ratio r: s is the ratio of the number of teeth of two connected gears. The ratio of the number of revolutions per minute (rpm) of two gear wheels is s: r. In the diagram below, Gear A is turned by a motor. The turning of Gear A causes Gears B and C to turn as well.

If Gear A is rotated by the motor at a rate of 100 rpm, what is the number of revolutions per minute for Gear C?
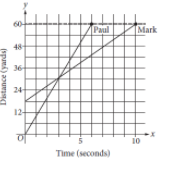
The graph above shows the positions of Paul and Mark during a race. Paul and Mark each ran at a constant rate, and Mark was given a head start to shorten the distance he needed to run. Paul finished the race in 6 seconds, and Mark finished the race in 10 seconds. According to the graph, Mark was given a head start of how many yards?
The graph of a y-intercept is the point at which the graph intersects the y-axis. We know that any point on the y-axis has an x-coordinate of 0. As a result, the x-coordinate of a y-intercept is 0.
The steps for determining the y-intercept of a function y = f (x),
• We simply replace x = 0 in it.
• Determine y.
• as the point, represent the y-intercept (0, y).
Here are some y-intercept examples.
• The y-intercept of y = 5x² + 2 is (0, 2) because we get y = 5(0)² + 2 = 2 when we substitute x = 0.
• The y-intercept of y = -5ex is (0, -5) because we get y = -5e0 = -5 when we substitute x = 0.

The graph above shows the positions of Paul and Mark during a race. Paul and Mark each ran at a constant rate, and Mark was given a head start to shorten the distance he needed to run. Paul finished the race in 6 seconds, and Mark finished the race in 10 seconds. According to the graph, Mark was given a head start of how many yards?
The graph of a y-intercept is the point at which the graph intersects the y-axis. We know that any point on the y-axis has an x-coordinate of 0. As a result, the x-coordinate of a y-intercept is 0.
The steps for determining the y-intercept of a function y = f (x),
• We simply replace x = 0 in it.
• Determine y.
• as the point, represent the y-intercept (0, y).
Here are some y-intercept examples.
• The y-intercept of y = 5x² + 2 is (0, 2) because we get y = 5(0)² + 2 = 2 when we substitute x = 0.
• The y-intercept of y = -5ex is (0, -5) because we get y = -5e0 = -5 when we substitute x = 0.
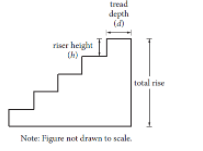
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway.
The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)
An architect can apply the riser-tread formula '2h + d = 25', where h is the height of the riser and d is the depth of tread in inches while creating a stairway. The riser heights and tread depths for every step in a staircase are the same for that staircase.
A stairway's riser count equals the number of steps it has. For instance, the stairs have five steps. A staircase's overall rise equals the sum of its riser heights.

When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway.
The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)
An architect can apply the riser-tread formula '2h + d = 25', where h is the height of the riser and d is the depth of tread in inches while creating a stairway. The riser heights and tread depths for every step in a staircase are the same for that staircase.
A stairway's riser count equals the number of steps it has. For instance, the stairs have five steps. A staircase's overall rise equals the sum of its riser heights.
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
|
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
|





