Physics-
General
Easy
Question
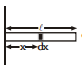
A closed cylinder of length 
containing a liquid of variable density 
. Find the net force exerted by the liquid on the axis of rotation. (Take the cylinder to be massless and A = cross sectional area of cylinder)
The correct answer is:
Related Questions to study
physics-
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 m 
, then the Young's modulus of the material of the wire is
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 m , then the Young's modulus of the material of the wire is
physics-General
physics-
A liquid of density r is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is 
. Now this tube is moved horizontally with acceleration 'a' as shown in the figure. During motion it is found that liquid in both column is at same level at equilibrium. If atmospheric pressure is 
, then value of is
A liquid of density r is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is . Now this tube is moved horizontally with acceleration 'a' as shown in the figure. During motion it is found that liquid in both column is at same level at equilibrium. If atmospheric pressure is , then value of is
physics-General
physics-
The tube shown is of non-uniform cross-section. The cross-section area at A is half of the cross-section area at B,C and D. A liquid is flowing through in steady state. The liquid exerts on the tube Statement I) A net force towards right. Statement II) A net force towards left. Statement III) A net force in some oblique direction. Statement IV) Zero net force Statement V) A net clockwise torque. Statement VI) A net counterclockwise torque
The tube shown is of non-uniform cross-section. The cross-section area at A is half of the cross-section area at B,C and D. A liquid is flowing through in steady state. The liquid exerts on the tube Statement I) A net force towards right. Statement II) A net force towards left. Statement III) A net force in some oblique direction. Statement IV) Zero net force Statement V) A net clockwise torque. Statement VI) A net counterclockwise torque
physics-General
physics-
A rigid ring A and a rigid thin disk B both made of same material, when gently placed on water, just manage to float due to surface tension as shown in the figure. Both the ring and the disk have same radius. What can you conclude about their masses?
A rigid ring A and a rigid thin disk B both made of same material, when gently placed on water, just manage to float due to surface tension as shown in the figure. Both the ring and the disk have same radius. What can you conclude about their masses?
physics-General
physics-
A cuboid 
is filled with two immiscible liquids of density 
as shown in the figure. Neglecting atmospheric pressure, ratio of force on base & side wall of the cuboid is
A cuboid is filled with two immiscible liquids of density as shown in the figure. Neglecting atmospheric pressure, ratio of force on base & side wall of the cuboid is
physics-General
physics-
An open vessel full of water is falling freely under gravity. There is a small hole in one face of the vessel, as shown in the figure. The water which comes out from the hole at the instant when hole is at height H above the ground, strikes the ground at a distance of x from P. Which of the following is correct for the situation described?
An open vessel full of water is falling freely under gravity. There is a small hole in one face of the vessel, as shown in the figure. The water which comes out from the hole at the instant when hole is at height H above the ground, strikes the ground at a distance of x from P. Which of the following is correct for the situation described?
physics-General
physics-
The pressure of water in a water pipe when tap is opened and closed is respectively 
and 
N
. With open tap, the velocity of water flowing is
The pressure of water in a water pipe when tap is opened and closed is respectively and N. With open tap, the velocity of water flowing is
physics-General
physics-
A large cylindrical tank of cross-sectional area 1 is filled with water. It has a small hole at a height of 1m from the bottom. A movable piston of mass 5 kg is fitted on the top of the tank such that it can slide in the tank freely. A load of 45 kg is applied on the top of water by piston, as shown in figure. The value of v when piston is 7m above the bottom is (g = 10 
)
A large cylindrical tank of cross-sectional area 1 is filled with water. It has a small hole at a height of 1m from the bottom. A movable piston of mass 5 kg is fitted on the top of the tank such that it can slide in the tank freely. A load of 45 kg is applied on the top of water by piston, as shown in figure. The value of v when piston is 7m above the bottom is (g = 10 )
physics-General
physics-
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by 
This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
Maximum height of the spacecraft above the surface of the Earth will be :
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
Maximum height of the spacecraft above the surface of the Earth will be :
physics-General
physics-
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
Semimajor axis of the new elliptical orbit is
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
Semimajor axis of the new elliptical orbit is
physics-General
physics-
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
If the spacecraft-earth system had initial energy (– 
), then the total mechanical energy of the system after firing the rocket will be :
Changing from a circular to An elliptical orbit Let us identify the system as the spacecraft and the Earth but not the portion of the fuel in the spacecraft that we use to change the orbit. In a given orbit, the mechanical energy of the spacecraft – Earth system is given by This energy includes the kinetic energy of the spacecraft and the potential energy associated with the gravitational force between the spacecraft and the Earth. If the rocket engines are fired, the thrust force moves the spacecraft through a displacement. As a result, the mechanical energy of the spacecraft – Earth system increases. The spacecraft has a new higher energy but is constrained to be in an orbit that includes the original starting point. It can not be in a higher energy circular orbit having a larger radius because this orbit would not contain the starting point. The only possibility is that the orbit is elliptical as shown in the figure.
If the spacecraft-earth system had initial energy (– ), then the total mechanical energy of the system after firing the rocket will be :
physics-General
physics-
STATEMENT-1 : In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum
STATEMENT-2 : When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing
STATEMENT-1 : In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum
STATEMENT-2 : When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing
physics-General
physics-
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. Then the magnitude of gravitational force exerted by earth on the rod is
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. Then the magnitude of gravitational force exerted by earth on the rod is
physics-General
physics-
A particle of mass M is at a distance 'a' from surface of a thin spherical shell of uniform equal mass and having radius a.
A particle of mass M is at a distance 'a' from surface of a thin spherical shell of uniform equal mass and having radius a.
physics-General
physics-
Gravitational field at the centre of a semicircle formed by a thin wire AB of mass m and length 
is :
Gravitational field at the centre of a semicircle formed by a thin wire AB of mass m and length is :
physics-General
