Question
Dana is riding in a 100 -mile-long bicycle race. The function  defined by f(x) = 100 - 18x models the number of miles that Dana has remaining
defined by f(x) = 100 - 18x models the number of miles that Dana has remaining  hours after she starts the race. What is the best interpretation of f(2) = 64 ?
hours after she starts the race. What is the best interpretation of f(2) = 64 ?
- Dana rides about 64 miles in the first 2 hours of the race.
- Dana will ride the last 64 miles of the race in about 2 hours.
- When Dana has ridden 64 miles, she has about 2 hours remaining.
- Two hours after Dana starts the race, she has about 64 miles remaining.
The correct answer is: Two hours after Dana starts the race, she has about 64 miles remaining.
HINT: From the given function, find the number of miles covered by Dana in each hour.
Complete step by step Sol.
Given function  models the number of miles that Dana has remaining
models the number of miles that Dana has remaining  hours after she starts the race.
hours after she starts the race.
Here, Dana goes 18 miles every hour. That is,
After riding for one hour Dana has covered only 18 miles.
That is when  She has 82 miles remaining. [
She has 82 miles remaining. [ ]
]
After the second hour, Dana has covered only 36 miles.
That is when  She has 64 miles remaining. [
She has 64 miles remaining. [ ]
]
So she has 64 miles remaining.
So, we can conclude that two hours after Dana starts the race, she has about 64 miles remaining.
Hence option D is the correct answer.
Related Questions to study
An advertising agency guarantees that its services will increase website traffic by 3.5% compared to each previous week. Which type of function best models the weekly guaranteed website traffic as the number of weeks increases?
An advertising agency guarantees that its services will increase website traffic by 3.5% compared to each previous week. Which type of function best models the weekly guaranteed website traffic as the number of weeks increases?
x + 2y = 10
2x – y = 5
The solution to the given system of equations is (x, y). What is the value of 3x + y ?
x + 2y = 10
2x – y = 5
The solution to the given system of equations is (x, y). What is the value of 3x + y ?
If 7x + 21 = - 2, what is the value of x + 3 ?
If 7x + 21 = - 2, what is the value of x + 3 ?
For the linear function f, f(2) = 10 and the graph of y = f(x) in the xy - plane has a slope of 3 . Which equation defines f ?
For the linear function f, f(2) = 10 and the graph of y = f(x) in the xy - plane has a slope of 3 . Which equation defines f ?
The scatterplot shows the relationship between two variables, x and y. A line of best fit is also shown.
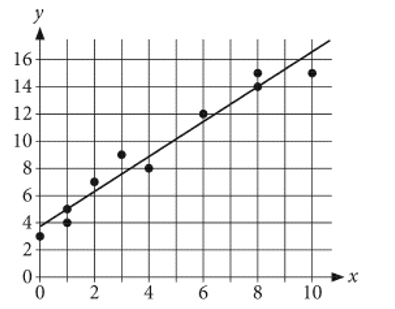
What is an equation of the line of best fit?
The scatterplot shows the relationship between two variables, x and y. A line of best fit is also shown.

What is an equation of the line of best fit?

For the linear function, f, the table shows several values of x and their corresponding values of f(x). What is the y- intercept of the graph of y = f(x) in the  -plane?
-plane?

For the linear function, f, the table shows several values of x and their corresponding values of f(x). What is the y- intercept of the graph of y = f(x) in the  -plane?
-plane?
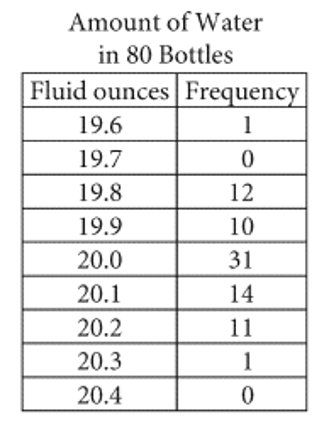
The frequency table above shows the distribution of the actual number of fluid ounces of water in a random sample of 8020 -ounce bottles of the water at a bottling plant. Bottles are only sold if they contain at least 19.8 but no more than 20.2 fluid ounces of water. If the proportion of bottles that can be sold is the same for the sample and the 16,000 20-ounce bottles produced at the plant each day, how many of the 16,000 bottles cannot be sold?

The frequency table above shows the distribution of the actual number of fluid ounces of water in a random sample of 8020 -ounce bottles of the water at a bottling plant. Bottles are only sold if they contain at least 19.8 but no more than 20.2 fluid ounces of water. If the proportion of bottles that can be sold is the same for the sample and the 16,000 20-ounce bottles produced at the plant each day, how many of the 16,000 bottles cannot be sold?
A local restaurant gives teachers a 20% discount on all their meals. If a teacher pays $14.00 for a meal after the discount was applied, what was the price of the meal before the discount?
A local restaurant gives teachers a 20% discount on all their meals. If a teacher pays $14.00 for a meal after the discount was applied, what was the price of the meal before the discount?
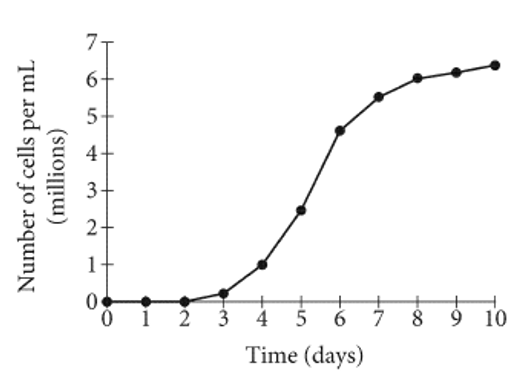
The graph shows the number of algae cells grown during an experiment, in millions of cells per milliliter (mL) of water, d days after the start of an experiment. Between which two days was the growth rate, in millions of cells per  of water per day, of the algae the greatest?
of water per day, of the algae the greatest?

The graph shows the number of algae cells grown during an experiment, in millions of cells per milliliter (mL) of water, d days after the start of an experiment. Between which two days was the growth rate, in millions of cells per  of water per day, of the algae the greatest?
of water per day, of the algae the greatest?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.