Question
Albedos of Various Earth Surfaces
An albedo is the amount of light reflected from a surface divided by the amount of light falling on the surface. The amount is typically measured in watts per square meter. The table shows the minimum and maximum albedos for different types of surfaces on Earth.
In a desert region, the amount of sunlight falling on a surface with an area of one square meter is 1,000 watts. Which of the following could be the amount of sunlight, in watts, reflected from this one-square-meter surface?
- 275
- 525
- 725
- 1,275
The correct answer is: 275
Amount of light falling is 1,000 watt/sq.m
Step 1:- find the maximum amount of light reflected
Given maximum albedo = 0.29 .
so maximum amount of light reflected is 0.29 ×1,000 = 290 watt/sq.m
Step 2:- find the minimum amount of light reflected
Given minimum albedo = 0.26 .
so minimum amount of light reflected is 0.26 ×1,000 = 260 watt/sq.m
So ,possible value of light reflected lies between 260 and 290 watt/sq.m
Option A (275 lies between 260 and 290 )
Related Questions to study
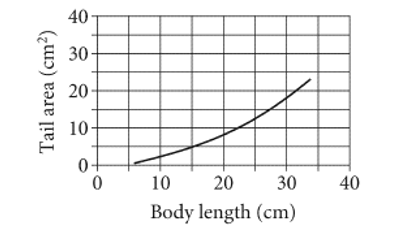
For a certain group of fish, the graph models the relationship between body length L, in centimeters (cm), and tail area A, in square centimeters 
, where 
. Which equation represents the relationship between body length and tail area?
Solving quadratic equations using a graph is an effective method for locating estimated solutions or roots for quadratic equations or functions.
The real roots of a quadratic function might be zero, one (repeated), or two. Finding the origins involves solving a quadratic equation with the right-hand side equal to zero, such as ax² + bx + c = 0.
Points to consider to solve a quadratic equation using a graph :
• Rearrange the equation so that one side corresponds to the graphed function.
• Plot the function y= the other side of the equation.
• To find the solutions, draw vertical lines down to the x-axis from the intersection points.
For a certain group of fish, the graph models the relationship between body length L, in centimeters (cm), and tail area A, in square centimeters , where . Which equation represents the relationship between body length and tail area?
Solving quadratic equations using a graph is an effective method for locating estimated solutions or roots for quadratic equations or functions.
The real roots of a quadratic function might be zero, one (repeated), or two. Finding the origins involves solving a quadratic equation with the right-hand side equal to zero, such as ax² + bx + c = 0.
Points to consider to solve a quadratic equation using a graph :
• Rearrange the equation so that one side corresponds to the graphed function.
• Plot the function y= the other side of the equation.
• To find the solutions, draw vertical lines down to the x-axis from the intersection points.
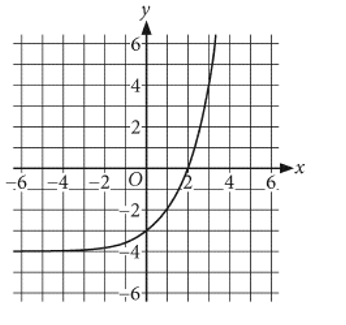
The graph of 
is shown, where a is a constant. What is the value of a ?
The graph of is shown, where a is a constant. What is the value of a ?
Which of the following is(are) an x - intercept of the graph of 
in the xy - plane?
I. (- 3,0)
II. (2, 0)
III. (0, 0)
Which of the following is(are) an x - intercept of the graph of in the xy - plane?
I. (- 3,0)
II. (2, 0)
III. (0, 0)
The function f is a linear function. The y - intercept of the graph of y = f(x) in the xy -plane is (0, - 12). What is the y-intercept of the graph of y = f(x) + 2 ?
The function f is a linear function. The y - intercept of the graph of y = f(x) in the xy -plane is (0, - 12). What is the y-intercept of the graph of y = f(x) + 2 ?
The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
In the xy-plane, line l has a slope of 2. Line k is perpendicular to line l and contains the point (4, 2). Which of the following is an equation of line k ?
In the xy-plane, line l has a slope of 2. Line k is perpendicular to line l and contains the point (4, 2). Which of the following is an equation of line k ?
In right triangle ABC, the length of side 
is 12 , the measure of 
is 
, and 
is a right angle. Which of the following can be determined using the information given?
I) The measure of 
II) The length of side 
Any triangle that has one 90-degree angle is said to have a right angle. Right triangles are those with an angle of 90 degrees, or "right angles," hence those with this angle. First, determine the third angle's measurement. You already know that C = 90 degrees because it is a right angle, and you are also aware of the size of A or B. Since a triangle's internal degree measurement must always equal 180 degrees, the third angle's measurement can be determined by applying the following formula: 180 – (90 + A) = B. The formula can also be turned around so that 180 - (90 + B) = A.
As an illustration, if you know that A is 40 degrees, then B is 180 – (90 – 40). It is easy to work out that B = 50 degrees if you simplify this to B = 180 - 130. Triangles can be resolved using the Law of Sines. Knowing the length of one side and the measurement of one other angle in addition to the right angle will especially assist you in finding the hypotenuse of a right triangle. The Law of Sines asserts that for any triangle with sides a, b, and c and angles a, b, and c, a / sin A = b / sin B = c / sin C.
Any triangle can be resolved using the Law of Sines, but only a right triangle will have a hypotenuse.
In right triangle ABC, the length of side is 12 , the measure of is , and is a right angle. Which of the following can be determined using the information given?
I) The measure of
II) The length of side
Any triangle that has one 90-degree angle is said to have a right angle. Right triangles are those with an angle of 90 degrees, or "right angles," hence those with this angle. First, determine the third angle's measurement. You already know that C = 90 degrees because it is a right angle, and you are also aware of the size of A or B. Since a triangle's internal degree measurement must always equal 180 degrees, the third angle's measurement can be determined by applying the following formula: 180 – (90 + A) = B. The formula can also be turned around so that 180 - (90 + B) = A.
As an illustration, if you know that A is 40 degrees, then B is 180 – (90 – 40). It is easy to work out that B = 50 degrees if you simplify this to B = 180 - 130. Triangles can be resolved using the Law of Sines. Knowing the length of one side and the measurement of one other angle in addition to the right angle will especially assist you in finding the hypotenuse of a right triangle. The Law of Sines asserts that for any triangle with sides a, b, and c and angles a, b, and c, a / sin A = b / sin B = c / sin C.
Any triangle can be resolved using the Law of Sines, but only a right triangle will have a hypotenuse.
?
What is the positive solution to the given equation?
