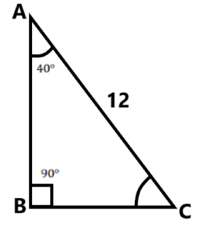
Question
In right triangle ABC, the length of side  is 12 , the measure of
is 12 , the measure of  is
is  , and
, and  is a right angle. Which of the following can be determined using the information given?
is a right angle. Which of the following can be determined using the information given?
I) The measure of 
II) The length of side 
- I only
- II only
- I and II
- Neither I nor II
The correct answer is: I and II
As stated in the problem statement,  is a right angle of right triangle ABC then,
is a right angle of right triangle ABC then,  is the hypotenuse. Consider the following diagram,
is the hypotenuse. Consider the following diagram,
Explanation:
Step 1 of 2:
Given,  ,
,  and
and  .
.
We know that the sum of all three angles of a triangle is  .
.
Here, 



The value of  is
is  .
.
Step 2 of 2:
We know that in a right triangle,  , where
, where  is the angle between hypotenuse and height of the triangle.
is the angle between hypotenuse and height of the triangle.
Thus, in the given  ,
, 

The measure of  is
is  .
.
Final Answer:
The right option is — I and II.
Any triangle that has one 90-degree angle is said to have a right angle. Right triangles are those with an angle of 90 degrees, or "right angles," hence those with this angle. First, determine the third angle's measurement. You already know that C = 90 degrees because it is a right angle, and you are also aware of the size of A or B. Since a triangle's internal degree measurement must always equal 180 degrees, the third angle's measurement can be determined by applying the following formula: 180 – (90 + A) = B. The formula can also be turned around so that 180 - (90 + B) = A.
As an illustration, if you know that A is 40 degrees, then B is 180 – (90 – 40). It is easy to work out that B = 50 degrees if you simplify this to B = 180 - 130. Triangles can be resolved using the Law of Sines. Knowing the length of one side and the measurement of one other angle in addition to the right angle will especially assist you in finding the hypotenuse of a right triangle. The Law of Sines asserts that for any triangle with sides a, b, and c and angles a, b, and c, a / sin A = b / sin B = c / sin C.
Any triangle can be resolved using the Law of Sines, but only a right triangle will have a hypotenuse.