Question
Let 
be such that 
and 
Then 
cannot satisfy
Hint:
In this question, we have to find the which region ϕ cannot satisfy. Now firstly, solve the given equation and find the value θ and ϕ and find the range of ϕ . If the given option is cannot match with the range then it will be our answer.
The correct answer is:
Here we have to find the which region ϕ cannot satisfy.
Now we have,
Given equation 
⇒2cosθ (1−sin ϕ) =sin2θ(
x cos ϕ)−1 [since, tan x + cot y = 2/sin2x]
⇒2cosθ−2cos
sin ϕ =2sinθcos ϕ −1
⇒2cosθ+1=2sin(θ+ ϕ) .....(i)
Also given that tan(2π−θ)>0
⇒tanθ<0.....(1)
−1<sinθ<− √3/2
⇒θ ϵ (3Π/2, 5Π/3) .....(2)
So, ′θ′ is in 4th quadrant ⇒ L.H.S. of equation (i) will be positive.
1<2cosθ+1<2
⇒1<2sin(θ+ ϕ)<2
⇒21<sin(θ ϕ)<1
⇒2π+π/6 < θ + ϕ < 5π/6 +2π
⇒ 2π +π/6 − θmax < ϕ <2π+ 5π/6 −θmin
⇒ π/2 < ϕ < 4π/3
Therefore, ϕ satisfy itself from π/2 to 4π/3 .
The correct answer is 0 < ϕ < 4π/3 , 3π/2 < ϕ < 2π and 4π/3 < ϕ < 3π/2.
In this question we have to find the the which region ϕ cannot satisfy. In this question more than one option is correct. Here firstly solve the given equation. Remember that, , tan x + cot x = 
.
Related Questions to study
The number of all possible values of , where 0< < 
, which the system of equations 
has a solution 
with 
, is
The number of all possible values of , where 0< < , which the system of equations has a solution with , is
Roots of the equation 
are
Roots of the equation are
Isomers are possible for the molecular formula
Isomers are possible for the molecular formula
The number of solutions of the pair of equations 
in the interval [0, 2] is
The number of solutions of the pair of equations in the interval [0, 2] is
Quantitative estimation of 
can be made by 
in acidified medium. In which medium it can be estimated by 
?
Quantitative estimation of can be made by in acidified medium. In which medium it can be estimated by ?
If 
then the value of 
is equal to
If then the value of is equal to
If 
, then the intervals of values of for which 
, is
If , then the intervals of values of for which , is
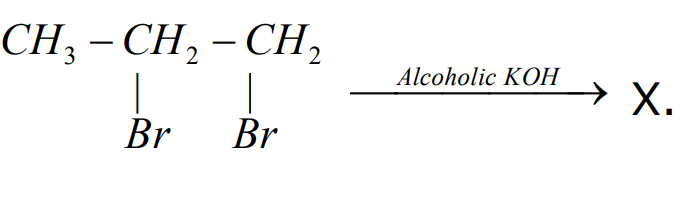. X is an unsaturated gaseous hydrocarbon. Find X?
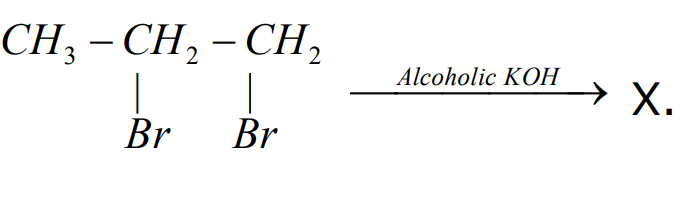. X is an unsaturated gaseous hydrocarbon. Find X?
The eq. wt. of 
in the reaction, 
is/are:
The eq. wt. of in the reaction, is/are:
Which statement(s) is/are wrong?
Which statement(s) is/are wrong?
To solve a trigonometric inequation of the type sin x ≥ a where |a| ≤ 1, we take a hill of length 2 in the sine curve and write the solution within that hill. For the general solution, we add 2n. For instance, to solve 
, we take the hill 
over which solution is 
The general solution is 
, n is any integer. Again to solve an inequation of the type sin x ≤ a, where |a| ≤ 1, we take a hollow of length 2 in the sine curve. (since on a hill, sinx ≤ a is satisfied over two intervals). Similarly cos x ≥ a or cosx ≤a, |a| ≤ 1 are solved.
Solution to the inequation 
must be
To solve a trigonometric inequation of the type sin x ≥ a where |a| ≤ 1, we take a hill of length 2 in the sine curve and write the solution within that hill. For the general solution, we add 2n. For instance, to solve , we take the hill over which solution is The general solution is , n is any integer. Again to solve an inequation of the type sin x ≤ a, where |a| ≤ 1, we take a hollow of length 2 in the sine curve. (since on a hill, sinx ≤ a is satisfied over two intervals). Similarly cos x ≥ a or cosx ≤a, |a| ≤ 1 are solved.
Solution to the inequation must be
Which of the following compounds does not give halo form reaction?
Which of the following compounds does not give halo form reaction?
is:
The product (A) is:
