Question
The point of contact of the line 2x – y + 2 = 0 with the parabola y2 = 16 x is-
- (3,4)
- (2,4)
- (1,4)
- (–2, 1)

substitute the values of a and m in the equation.
The correct answer is: (1,4)
1,4
point of contact of the tangent = (a/m2, 2a/m) = (4/22, 8/2) = (1,4)
for a line to be a tangent of a parabola, the value of a/m should be equal to the value of c.
Related Questions to study
The point on the curve y2 = x the tangent at which makes an angle of 45º with x-axis will be given by
the point of contact of a tangent with the curve is given by (x,y) =(a/m2, 2a/m). this is obtained by solving the equation of tangent with the equation of curve.
The point on the curve y2 = x the tangent at which makes an angle of 45º with x-axis will be given by
the point of contact of a tangent with the curve is given by (x,y) =(a/m2, 2a/m). this is obtained by solving the equation of tangent with the equation of curve.
The equation of the tangent to the parabola y = 2 + 4x –4x2 with slope –4 is
equation of a straight line : y-y1=m(x-x1)
m is given, calculate x1 and y1 by differentiating the equation of parabola and equating it with the slope.
The equation of the tangent to the parabola y = 2 + 4x –4x2 with slope –4 is
equation of a straight line : y-y1=m(x-x1)
m is given, calculate x1 and y1 by differentiating the equation of parabola and equating it with the slope.
The equation of the tangent at vertex to the parabola 4y2 + 6x = 8y + 7 is
if the slope of a line is infinite, then it is parallel to the y axis and the equation becomes x=a, where x is the x intercept.
Slope of the tangent : dy/dx
The equation of the tangent at vertex to the parabola 4y2 + 6x = 8y + 7 is
if the slope of a line is infinite, then it is parallel to the y axis and the equation becomes x=a, where x is the x intercept.
Slope of the tangent : dy/dx
The point where the line x + y = 1 touches the parabola y = x– x2 , is-
the point of intersection of two curves can be found out by solving the equations of the two curves,
The point where the line x + y = 1 touches the parabola y = x– x2 , is-
the point of intersection of two curves can be found out by solving the equations of the two curves,
The equation of the tangent to the parabola y2 = 4x at the point (1, 2) is-
Slope of tangent = dy/dx
Equation of line: y-y1 = m(x-x1)
The equation of the tangent to the parabola y2 = 4x at the point (1, 2) is-
Slope of tangent = dy/dx
Equation of line: y-y1 = m(x-x1)
If a tangent to the parabola 4y2 = x makes an angle of 60º with the x- axis, then its point of contact is-
point of contact = (a/m2, 2a/m)
slope = tan ( angle made with the x axis)
this gives us the value of m
y^2 = x/4 = 4(1/16)x
a = 1/16
If a tangent to the parabola 4y2 = x makes an angle of 60º with the x- axis, then its point of contact is-
point of contact = (a/m2, 2a/m)
slope = tan ( angle made with the x axis)
this gives us the value of m
y^2 = x/4 = 4(1/16)x
a = 1/16
At which point the line x = my +  touches the parabola x2 =4ay
touches the parabola x2 =4ay
the point of contact is the point of intersection between the 2 curves, the parabola and the line. this can be obtained by solving the two equations.
At which point the line x = my +  touches the parabola x2 =4ay
touches the parabola x2 =4ay
the point of contact is the point of intersection between the 2 curves, the parabola and the line. this can be obtained by solving the two equations.
For what value of k, the line 2y – x + k = 0 touches the parabola x2 + 4y = 0-
when a quadratic equation has 2 equal roots, the D value is 0 . D= b^2 - 4ac.=0
this gives us the possible value(s) of k
For what value of k, the line 2y – x + k = 0 touches the parabola x2 + 4y = 0-
when a quadratic equation has 2 equal roots, the D value is 0 . D= b^2 - 4ac.=0
this gives us the possible value(s) of k
An element, X has the following isotopic composition, 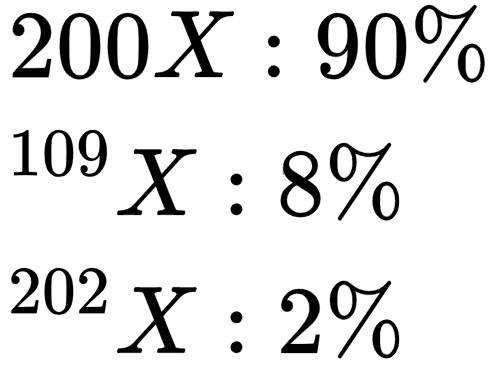 the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
An element, X has the following isotopic composition, 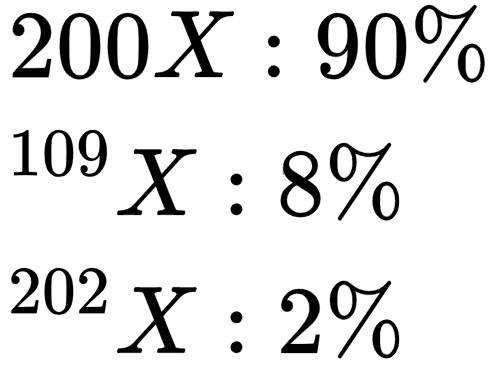 the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
The line  x + my + n = 0 will touch the parabola y2 = 4ax, if
x + my + n = 0 will touch the parabola y2 = 4ax, if
a quadratic equation has equal roots if the D value is zero. this is the condition of the line touching the curve.
The line  x + my + n = 0 will touch the parabola y2 = 4ax, if
x + my + n = 0 will touch the parabola y2 = 4ax, if
a quadratic equation has equal roots if the D value is zero. this is the condition of the line touching the curve.
The straight line 2x + y –1= 0 meets the parabola y2 = 4x in
when D> 0, two real and distinct roots
when D=0, real and equal roots
when D<0 imaginary roots.
The straight line 2x + y –1= 0 meets the parabola y2 = 4x in
when D> 0, two real and distinct roots
when D=0, real and equal roots
when D<0 imaginary roots.
The line y = mx + c may touch the parabola y2 = 4a (x + a), if-
the solution of the two curves gives us the quadratic equation. D=0 gives us the required answer.
The line y = mx + c may touch the parabola y2 = 4a (x + a), if-
the solution of the two curves gives us the quadratic equation. D=0 gives us the required answer.
The straight line x + y = k touches the parabola y = x – x2, if k =
since only one point of contact is present, D=0 gives the real root.
The straight line x + y = k touches the parabola y = x – x2, if k =
since only one point of contact is present, D=0 gives the real root.
If the line x + y –1 = 0 touches the parabola y2 = kx, then the value of k is-
we can also solve for the two lines and make the D=0 for the resultant quadratic equation.
If the line x + y –1 = 0 touches the parabola y2 = kx, then the value of k is-
we can also solve for the two lines and make the D=0 for the resultant quadratic equation.
If length of the two segments of focal chord to the parabola y2 = 8ax are 2 and 4, then the value of a is-
the harmonic mean of the lengths (PS,QS) where S is the focus is equal to the half of latus rectum
the parametric coordinates of the ends of focal chords are (at^2, 2at) and (a/t^2,-2a/t)
If length of the two segments of focal chord to the parabola y2 = 8ax are 2 and 4, then the value of a is-
the harmonic mean of the lengths (PS,QS) where S is the focus is equal to the half of latus rectum
the parametric coordinates of the ends of focal chords are (at^2, 2at) and (a/t^2,-2a/t)



