Question
x + 2y = 10
2x – y = 5
The solution to the given system of equations is (x, y). What is the value of 3x + y ?
- 5
- 7
- 13
- 15
The correct answer is: 15
HINT: Solve the system of equations.
Complete step by step Solution
Given system of equations are,
 (i)
(i)
 …(ii)
…(ii)
Multiply (i) with 2 to make the coefficients of  to be the same in both the equations.
to be the same in both the equations.
On multiplying, we get  …(iii)
…(iii)
On subtracting (ii) from (iii),
We get LHS to be 
And RHS to be 
On equating LHS and RHS,
we get y = 3.
On substituting  in (i),
in (i),
We get,  .
.
So the value of 
Therefore, 
Hence option D is the correct answer.
Note: We can solve this directly by adding these 2 equations. Then LHS would be  and RHS would be 15. Hence we get
and RHS would be 15. Hence we get  .
.
Related Questions to study
If 7x + 21 = - 2, what is the value of x + 3 ?
If 7x + 21 = - 2, what is the value of x + 3 ?
For the linear function f, f(2) = 10 and the graph of y = f(x) in the xy - plane has a slope of 3 . Which equation defines f ?
For the linear function f, f(2) = 10 and the graph of y = f(x) in the xy - plane has a slope of 3 . Which equation defines f ?
The scatterplot shows the relationship between two variables, x and y. A line of best fit is also shown.
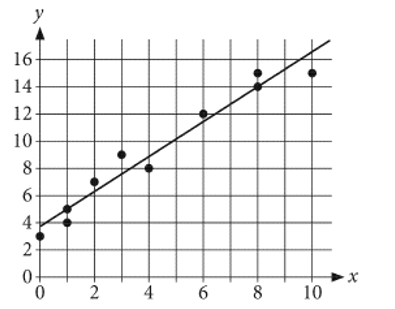
What is an equation of the line of best fit?
The scatterplot shows the relationship between two variables, x and y. A line of best fit is also shown.

What is an equation of the line of best fit?

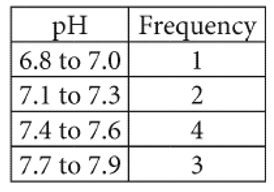
For the linear function, f, the table shows several values of x and their corresponding values of f(x). What is the y- intercept of the graph of y = f(x) in the  -plane?
-plane?

For the linear function, f, the table shows several values of x and their corresponding values of f(x). What is the y- intercept of the graph of y = f(x) in the  -plane?
-plane?
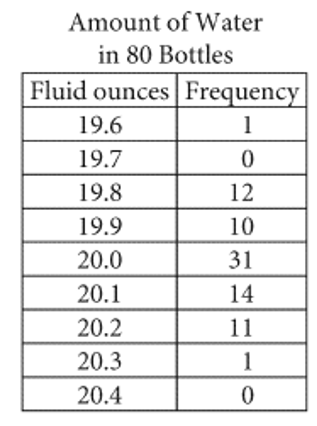
The frequency table above shows the distribution of the actual number of fluid ounces of water in a random sample of 8020 -ounce bottles of the water at a bottling plant. Bottles are only sold if they contain at least 19.8 but no more than 20.2 fluid ounces of water. If the proportion of bottles that can be sold is the same for the sample and the 16,000 20-ounce bottles produced at the plant each day, how many of the 16,000 bottles cannot be sold?

The frequency table above shows the distribution of the actual number of fluid ounces of water in a random sample of 8020 -ounce bottles of the water at a bottling plant. Bottles are only sold if they contain at least 19.8 but no more than 20.2 fluid ounces of water. If the proportion of bottles that can be sold is the same for the sample and the 16,000 20-ounce bottles produced at the plant each day, how many of the 16,000 bottles cannot be sold?
A local restaurant gives teachers a 20% discount on all their meals. If a teacher pays $14.00 for a meal after the discount was applied, what was the price of the meal before the discount?
A local restaurant gives teachers a 20% discount on all their meals. If a teacher pays $14.00 for a meal after the discount was applied, what was the price of the meal before the discount?
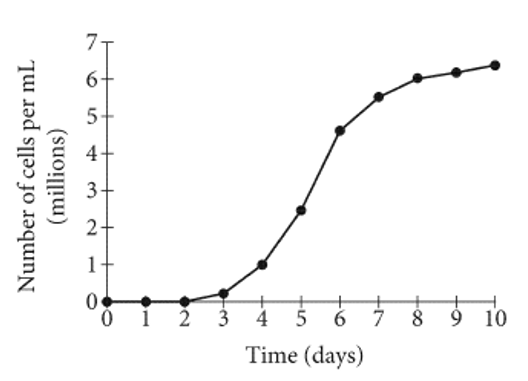
The graph shows the number of algae cells grown during an experiment, in millions of cells per milliliter (mL) of water, d days after the start of an experiment. Between which two days was the growth rate, in millions of cells per  of water per day, of the algae the greatest?
of water per day, of the algae the greatest?

The graph shows the number of algae cells grown during an experiment, in millions of cells per milliliter (mL) of water, d days after the start of an experiment. Between which two days was the growth rate, in millions of cells per  of water per day, of the algae the greatest?
of water per day, of the algae the greatest?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance d, in miles, Haimi drove as a function of the time t, in hours, since she started driving is modeled by the equation d = 60t.
What interval represents all values of  during which Haimi drove in North Dakota?
during which Haimi drove in North Dakota?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
Haimi drove a car from West Union, Minnesota, through North Dakota, to Miles City, Montana. The total distance she traveled through each state is shown in the figure.

The distance  , in miles, Haimi drove as a function of the time
, in miles, Haimi drove as a function of the time  , in hours, since she started driving is modeled by the equation d = 60t.
, in hours, since she started driving is modeled by the equation d = 60t.
According to the model, what distance, in miles, had Haimi driven 3 hours after she started driving?
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.
The probability of an unfair coin landing heads side up is 0.6. A student tossed this coin into the air 9 times. It landed tails side up 5 times and heads side up 4 times. What is the probability that the coin will land heads side up on the 10th toss?
When a coin is flipped, it has unequal chances of landing heads-up or tails-up. • A Bernoulli trial is a random experiment with two possible outcomes, which are commonly referred to as success and failure, or the numeric values 1 and 0.
A fair coin has one tail and one head. Both of these outcomes have an equal chance of being the event's final outcome. For an unfair coin, the probability of seeing heads is 2/2 or 1. Similarly, the likelihood of a tail on an unfair coin is 2/2 or 1.
When a coin does not behave like a standard coin, it is said to be an Unfair Coin. Unfair Coin does not have the same outputs as a regular coin, for example, an Unfair Coin has either two heads or two tails.