Question
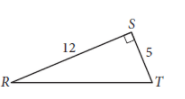
In triangle RST above, point W (not shown) lies on  . What is the value of cos(∠RSW) − sin(∠WST) ?
. What is the value of cos(∠RSW) − sin(∠WST) ?
The correct answer is: 0
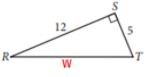
The diagram above is a right-angle triangle and can be seen when the image is straightened
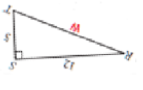
Line RT = w
Since triangle RST is a right angle triangle, w can be found using Pythagoras theorem:
hyp2 = opp2 + adj2
opp which stands for opposite, is the side opposite to the angle
hyp which stands for hypotenuse, is the longest side
adj stands for adjacent
Thus, w2 = 122 + 52
w2 = 144 + 25
w2 = 169
Take square root of both sides,
w = 13
cos(∠RSW) = adj/hyp = 12/13
sin (∠WST) = opp/hyp = 12/13
12/13 – 12/13
= 0
Related Questions to study

If x = 1 in the equation above, what is the value of a ?

If x = 1 in the equation above, what is the value of a ?
(x − 6)2 + (y + 5)2 = 16
In the xy-plane, the graph of the equation above is a circle. Point P is on the circle and has coordinates (10, −5). If  is a diameter of the circle, what are the coordinates of point Q ?
is a diameter of the circle, what are the coordinates of point Q ?
(x − 6)2 + (y + 5)2 = 16
In the xy-plane, the graph of the equation above is a circle. Point P is on the circle and has coordinates (10, −5). If  is a diameter of the circle, what are the coordinates of point Q ?
is a diameter of the circle, what are the coordinates of point Q ?
f (x) = x3 - 9x
g(x) = x2 - 2x - 3
Which of the following expressions is equivalent to  ?
?
f (x) = x3 - 9x
g(x) = x2 - 2x - 3
Which of the following expressions is equivalent to  ?
?
|
x |
g(x) |
|
-2 |
1 |
|
-1 |
2 |
|
0 |
3 |
|
1 |
4 |
|
2 |
5 |
|
3 |
6 |
|
4 |
7 |
|
x |
g(x) |
|
-2 |
1 |
|
-1 |
2 |
|
0 |
3 |
|
1 |
4 |
|
2 |
5 |
|
3 |
6 |
|
4 |
7 |
Volume 
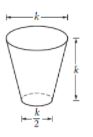
The glass pictured above can hold a maximum volume of 473 cubic centimeters, which is approximately 16 fluid ounces.
Jenny has a pitcher that contains 1 gallon of water. How many times could Jenny completely fill the glass with 1 gallon of water? (1 gallon = 128 fluid ounces)
Volume 

The glass pictured above can hold a maximum volume of 473 cubic centimeters, which is approximately 16 fluid ounces.
Jenny has a pitcher that contains 1 gallon of water. How many times could Jenny completely fill the glass with 1 gallon of water? (1 gallon = 128 fluid ounces)
In the xy-plane, the point (p, r) lies on the line with equation y = x + b, where b is a constant. The point with coordinates (2p, 5r) lies on the line with equation y = 2x + b. If p ≠ 0, what is the value of  ?
?
If we have coordinates of two points on a line, then we can use the slope formula to determine that line's slope. m = (y2-y1) / (x2-x1), or the ratio of the change in the y values and the x values, is the slope formula. 'x1' and 'y1' are the coordinates of the first point. The second points have the coordinates x2 and y2. If you have two points, you can always calculate the slope of a line. If you don't have access to two points, you can locate two points on the graph and use those to calculate the slope.
¶Observe the following helpful information:
- m = slope
¶-Rise = the difference between the y-values (y2 - y1), where (x1, y1) = point 1 and (x2, y2) = point 2.
Run is equal to the difference between x-values (x2 - x1).
In the xy-plane, the point (p, r) lies on the line with equation y = x + b, where b is a constant. The point with coordinates (2p, 5r) lies on the line with equation y = 2x + b. If p ≠ 0, what is the value of  ?
?
If we have coordinates of two points on a line, then we can use the slope formula to determine that line's slope. m = (y2-y1) / (x2-x1), or the ratio of the change in the y values and the x values, is the slope formula. 'x1' and 'y1' are the coordinates of the first point. The second points have the coordinates x2 and y2. If you have two points, you can always calculate the slope of a line. If you don't have access to two points, you can locate two points on the graph and use those to calculate the slope.
¶Observe the following helpful information:
- m = slope
¶-Rise = the difference between the y-values (y2 - y1), where (x1, y1) = point 1 and (x2, y2) = point 2.
Run is equal to the difference between x-values (x2 - x1).





