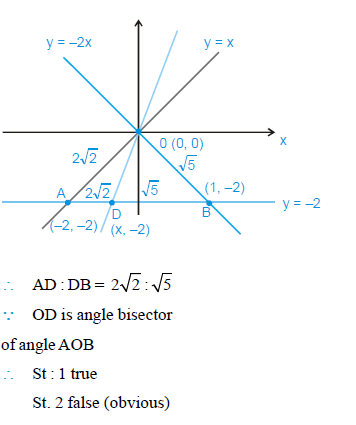
The line and intersect the line at P and Q respectively. The bisector of the acute angle between L₁ and L₂ intersects L₃ at R
Statement - 1 : The ratio PR : RQ equals
Statement - 2 : In any triangle, bisector of an angle divides the triangle into two similar triangles.

If one of the lines given by is 3x + 4y = 0, then c equals :

If the sum of first natural numbers is 1/5 times the sum of their squares, then the value of is

If , then the value of x in terms of y is

Given the lines y + 2x = 3 and y + 2x = 5 cut the axes at A, B and C, D respectively.
Statement- I ABDC forms quadrilateral and point (2, 3) lies inside the quadrilateral
Statement- II Point lies on same side of the lines.

The x-coordinates of the vertices of a square of unit area are the roots of the equation and the y-coordinates of the vertices are the roots of the equation then the possible vertices of the square is/are :

therefore the possible vertices of the square are (1,1),(1,2),(2,1),(2,2) and  (−1,1),(−1,2),(−2,2),(−2,1)

The straight lines x + y = 0, 3x + y - 4 = 0 and x + 3y -4 = 0 form a triangle which is

therefore it forms an isosceles triangle

Equation of a straight line passing through the point (4, 5) and equally inclined to the lines 3x = 4y + 7 and 5y = 12x + 6 is

If the equation represents a pair of lines whose slopes are m and , then value(s) of a is/are -

The curve passing through the points of intersection of and represents a pair of straight lines which are

The number of divisors of and are in

The equation of perpendicular bisector of the line segment joining the points (1, 2) and (–2, 0) is -

If are in

An infinite GP has first term and sum 5, then

Area of a triangle whose vertices are is

In a geometric progression (GP) the ratio of the sum of the first three terms and first six terms is 125:152 the common ratio is