Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

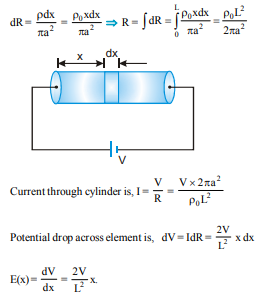
A cylindrical solid of length L and radius a is having varying resistivity given by r = r0 x where r0 is a positive constant and x is measured from left end of solid. The cell shown in the figure is having emf V and negligible internal resistance. The electric field as a function of x is best described by :

$\frac{2 V}{L^{2}} \times x$
$\frac{2 V}{ρ_{0} L^{2}} \times x$
$\frac{V}{L^{2}} \times x$
None of these

The correct answer is: $fraction numerator 2 V over denominator L to the power of 2 end exponent end fraction cross times x$

Consider an elemental part of solid at a distance x from left end of width dx. Resistance of this elemental part is

Related Questions to study

A charged oil drop falls with terminal velocity V₀ in the absence of electric field An electric field E keeps it stationary The drop acquires additional charge q and starts moving upwards with velocity V₀ The initial charge on the drop was

A charged oil drop falls with terminal velocity V₀ in the absence of electric field An electric field E keeps it stationary The drop acquires additional charge q and starts moving upwards with velocity V₀ The initial charge on the drop was

physics-General

if $ell parallel to m$ find the value of x in given figure.

if $ell parallel to m$ find the value of x in given figure.

The number of positive integral solutions of the inequation $fraction numerator x squared left parenthesis 3 x minus 4 right parenthesis cubed left parenthesis x minus 2 right parenthesis to the power of 4 over denominator left parenthesis x minus 5 right parenthesis to the power of 5 left parenthesis 2 x minus 7 right parenthesis to the power of 6 end fraction less or equal than 0$ is –

The number of positive integral solutions of the inequation $fraction numerator x squared left parenthesis 3 x minus 4 right parenthesis cubed left parenthesis x minus 2 right parenthesis to the power of 4 over denominator left parenthesis x minus 5 right parenthesis to the power of 5 left parenthesis 2 x minus 7 right parenthesis to the power of 6 end fraction less or equal than 0$ is –

parallel

Set of values of x satisfying the inequality $fraction numerator left parenthesis x minus 3 right parenthesis squared left parenthesis 2 x plus 5 right parenthesis squared left parenthesis x minus 7 right parenthesis over denominator open parentheses x squared plus x plus 1 close parentheses left parenthesis 3 x plus 6 right parenthesis squared end fraction less or equal than 0$ is $left square bracket a comma b right parenthesis union left parenthesis b comma c right square bracket$ then 2a + b + c is equal to

Set of values of x satisfying the inequality $fraction numerator left parenthesis x minus 3 right parenthesis squared left parenthesis 2 x plus 5 right parenthesis squared left parenthesis x minus 7 right parenthesis over denominator open parentheses x squared plus x plus 1 close parentheses left parenthesis 3 x plus 6 right parenthesis squared end fraction less or equal than 0$ is $left square bracket a comma b right parenthesis union left parenthesis b comma c right square bracket$ then 2a + b + c is equal to

Number of integral values of x for which the inequality log₁₀ $open parentheses fraction numerator 2 x minus 2007 over denominator x plus 1 end fraction close parentheses$ $less or equal than$ 0 holds true, is

Number of integral values of x for which the inequality log₁₀ $open parentheses fraction numerator 2 x minus 2007 over denominator x plus 1 end fraction close parentheses$ $less or equal than$ 0 holds true, is

$x to the power of log subscript 5 invisible function application x end exponent greater than 5$ implies

$x to the power of log subscript 5 invisible function application x end exponent greater than 5$ implies

parallel

log4 (2x2 + x + 1) – log² (2x – 1) $less or equal than$ – tan $fraction numerator 7 pi over denominator 4 end fraction$

log4 (2x2 + x + 1) – log² (2x – 1) $less or equal than$ – tan $fraction numerator 7 pi over denominator 4 end fraction$

The solution set of the inequation log1/3 (x² + x + 1) + 1 > 0 is

The solution set of the inequation log1/3 (x² + x + 1) + 1 > 0 is

If $open parentheses a to the power of log subscript b end subscript invisible function application x end exponent close parentheses to the power of 2 end exponent$ –5 $x to the power of log subscript b end subscript invisible function application a end exponent$ + 6 = 0 where a > 0, b > 0 & ab $not equal to$ 1. Then the value of x is equal to

If $open parentheses a to the power of log subscript b end subscript invisible function application x end exponent close parentheses to the power of 2 end exponent$ –5 $x to the power of log subscript b end subscript invisible function application a end exponent$ + 6 = 0 where a > 0, b > 0 & ab $not equal to$ 1. Then the value of x is equal to

parallel

No. of ordered pair satisfying simultaneously the system of equation $2 to the power of square root of x end exponent$ . $2 to the power of square root of y end exponent$ = 256 & log10 $square root of x y end root$ – log10 1.5 = 1 is.

No. of ordered pair satisfying simultaneously the system of equation $2 to the power of square root of x end exponent$ . $2 to the power of square root of y end exponent$ = 256 & log10 $square root of x y end root$ – log10 1.5 = 1 is.

If $x to the power of left square bracket log subscript 3 end subscript invisible function application x to the power of 2 end exponent plus left parenthesis log subscript 3 end subscript invisible function application x right parenthesis to the power of 2 end exponent minus 10 right square bracket end exponent$ = 1/x², then x =

If $x to the power of left square bracket log subscript 3 end subscript invisible function application x to the power of 2 end exponent plus left parenthesis log subscript 3 end subscript invisible function application x right parenthesis to the power of 2 end exponent minus 10 right square bracket end exponent$ = 1/x², then x =

If x_n > x_n–1>...> x₂ > x₁ > 1 then the value of $log subscript straight x subscript 1 end subscript invisible function application log subscript straight x subscript 2 end subscript invisible function application log subscript straight x subscript 3 end subscript invisible function application horizontal ellipsis log subscript straight x subscript straight n end subscript invisible function application x subscript n$ $blank to the power of x subscript n minus 1 end subscript superscript up right diagonal ellipsis to the power of x subscript 1 end exponent end superscript end exponent$ is equal to-

If x_n > x_n–1>...> x₂ > x₁ > 1 then the value of $log subscript straight x subscript 1 end subscript invisible function application log subscript straight x subscript 2 end subscript invisible function application log subscript straight x subscript 3 end subscript invisible function application horizontal ellipsis log subscript straight x subscript straight n end subscript invisible function application x subscript n$ $blank to the power of x subscript n minus 1 end subscript superscript up right diagonal ellipsis to the power of x subscript 1 end exponent end superscript end exponent$ is equal to-

parallel

The expression logp 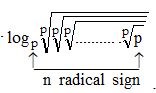where $p greater or equal than 2 comma p element of N semicolon n element of N$ when simplified is.

The expression logp where $p greater or equal than 2 comma p element of N semicolon n element of N$ when simplified is.

Let N= $open parentheses open parentheses square root of 7 close parentheses to the power of fraction numerator 2 over denominator log subscript 25 end subscript invisible function application 7 end fraction end exponent minus 12 5 to the power of log subscript 25 end subscript invisible function application 6 end exponent close parentheses$ Then log₂N has the value –

Let N= $open parentheses open parentheses square root of 7 close parentheses to the power of fraction numerator 2 over denominator log subscript 25 end subscript invisible function application 7 end fraction end exponent minus 12 5 to the power of log subscript 25 end subscript invisible function application 6 end exponent close parentheses$ Then log₂N has the value –

If a² + 4b² = 12ab, then log (a + 2b) =

If a² + 4b² = 12ab, then log (a + 2b) =

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.