Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

The angle between ax + by + c = 0 and (a + b) x – (a – b) y = 0 is

30°
45°
60°
90°

hint Hint:

First, we will find the slopes of the lines. The slope of a line $a x plus b y plus c space equals 0$ is given by $m space equals space fraction numerator negative space c o e f f i c i e n t space o f space y space over denominator c o e f f i c i e n t space o f space x end fraction$ . After that we will use the formula of the angle between the two lines $tan open parentheses theta close parentheses equals open vertical bar fraction numerator m subscript 1 minus m subscript 2 over denominator 1 plus m subscript 1 m subscript 2 end fraction close vertical bar$ where $m subscript 1$ and $m subscript 2$ are the slope of the lines and $theta$ is the angle between the lines.

The correct answer is: 45°

The formula of the angle between the two lines is given by
$tan open parentheses theta close parentheses equals open vertical bar fraction numerator m subscript 1 minus m subscript 2 over denominator 1 plus m subscript 1 m subscript 2 end fraction close vertical bar$ where $m subscript 1$ and $m subscript 2$ are the slope of the lines and $theta$ is the angle between the lines.
Step1: Finding the Slopes of the lines.
The slope of a line $a x plus b y plus c space equals 0$ is given by $m space equals space fraction numerator negative space c o e f f i c i e n t space o f space y space over denominator c o e f f i c i e n t space o f space x end fraction$ hence, $m equals fraction numerator negative b over denominator a end fraction$ .
Therefore slopes of the given lines are $m subscript 1 equals fraction numerator negative b over denominator a end fraction$ and $m subscript 2 equals fraction numerator negative left parenthesis negative left parenthesis a minus b right parenthesis right parenthesis over denominator left parenthesis a plus b right parenthesis end fraction$
Step2: Finding the angles between the lines.
$tan open parentheses theta close parentheses equals open vertical bar fraction numerator m subscript 1 minus m subscript 2 over denominator 1 plus m subscript 1 m subscript 2 end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style fraction numerator negative b over denominator a end fraction end style minus begin display style fraction numerator left parenthesis a minus b right parenthesis over denominator a plus b end fraction end style over denominator 1 plus left parenthesis begin display style fraction numerator negative b over denominator a end fraction end style cross times begin display style fraction numerator left parenthesis a minus b right parenthesis over denominator left parenthesis a plus b right parenthesis end fraction end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style fraction numerator negative b cross times left parenthesis a plus b right parenthesis minus a cross times left parenthesis a minus b right parenthesis over denominator a left parenthesis a plus b right parenthesis end fraction end style over denominator begin display style fraction numerator a cross times left parenthesis a plus b right parenthesis minus b cross times left parenthesis a minus b right parenthesis over denominator a left parenthesis a plus b right parenthesis end fraction end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style negative b cross times left parenthesis a plus b right parenthesis minus a cross times left parenthesis a minus b right parenthesis end style over denominator begin display style a cross times left parenthesis a plus b right parenthesis minus b cross times left parenthesis a minus b right parenthesis end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style left parenthesis negative a b minus b squared minus a squared plus a b right parenthesis end style over denominator begin display style left parenthesis a squared plus a b minus a b plus b squared right parenthesis end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style left parenthesis negative b squared minus a squared right parenthesis end style over denominator begin display style left parenthesis a squared plus b squared right parenthesis end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar fraction numerator begin display style negative left parenthesis a squared plus b squared right parenthesis end style over denominator begin display style left parenthesis a squared plus b squared right parenthesis end style end fraction close vertical bar$
=> $tan open parentheses theta close parentheses equals open vertical bar negative 1 close vertical bar space equals greater than 1$
So $theta equals 45 to the power of ring operator$

Related Questions to study

If a line perpendicular to 2x - 3y + 7 = 0 forms a triangle with the coordinate axes whose area is 3 sq. units, then the equation of the line (s) is

If a line perpendicular to 2x - 3y + 7 = 0 forms a triangle with the coordinate axes whose area is 3 sq. units, then the equation of the line (s) is

For all value of a and b the line ( a + 2b) x + (a - b) y + (a + 5b) = 0 passes through the point

For all value of a and b the line ( a + 2b) x + (a - b) y + (a + 5b) = 0 passes through the point

Equation of the line making equal intercepts on the axes and passing through the point (2, 4) is

Equation of the line making equal intercepts on the axes and passing through the point (2, 4) is

parallel

The equation of the line passing through (3, –4) and perpendicular to the line joining (–2, 6) and (5, 9) is

The equation of the line passing through (3, –4) and perpendicular to the line joining (–2, 6) and (5, 9) is

A line make zero intercepts on x – axis and y – axis and it is perpendicular to the line 3x +4y+ 6 = 0 then its equation is

A line make zero intercepts on x – axis and y – axis and it is perpendicular to the line 3x +4y+ 6 = 0 then its equation is

As shown in the diagram, points $p subscript 1 end subscript comma p subscript 2 end subscript comma p subscript 3 end subscript horizontal ellipsis horizontal ellipsis horizontal ellipsis. p subscript 10 end subscript$ are either the Then the number of groups of four points

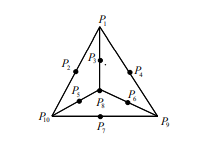
$open parentheses p subscript 1 end subscript comma p subscript i end subscript comma p subscript j end subscript comma p subscript k end subscript close parentheses left parenthesis 1 less than i less than j less than k £ 10 right parenthesis$ on the same plane is.

As shown in the diagram, points $p subscript 1 end subscript comma p subscript 2 end subscript comma p subscript 3 end subscript horizontal ellipsis horizontal ellipsis horizontal ellipsis. p subscript 10 end subscript$ are either the Then the number of groups of four points

$open parentheses p subscript 1 end subscript comma p subscript i end subscript comma p subscript j end subscript comma p subscript k end subscript close parentheses left parenthesis 1 less than i less than j less than k £ 10 right parenthesis$ on the same plane is.

parallel

Which of the following belongs to, e.g. (double grade) orbitals?

Which of the following belongs to, e.g. (double grade) orbitals?

Chemistry-General

Reduce $48 over 56$ into lowest from

Reduce $48 over 56$ into lowest from

Find the area of the triangle with base 30 cm and height 15cm.

Find the area of the triangle with base 30 cm and height 15cm.

parallel

The eccentricity of an ellipse whose centre is at the origin is $1 half space$ If one of its directrices is $x equals negative 4$ then the equation of the normal to it at $open parentheses 1 comma fraction numerator 3 over denominator 2 end fraction close parentheses text end text$ is

The eccentricity of an ellipse whose centre is at the origin is $1 half space$ If one of its directrices is $x equals negative 4$ then the equation of the normal to it at $open parentheses 1 comma fraction numerator 3 over denominator 2 end fraction close parentheses text end text$ is

Find the mean absolute deviation of the given numbers: 6,10,3,3,5,8,6,2

Find the mean absolute deviation of the given numbers: 6,10,3,3,5,8,6,2

Use counter to add -5 + 2, where is + and Is –
Start with:
You add:
Which picture shows the sum:

Use counter to add -5 + 2, where is + and Is –
Start with:
You add:
Which picture shows the sum:

parallel

The line $∣ x plus m y plus n equals 0 text end text$ is a normal to the ellipse $text end text fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1 text end text$ is

The line $∣ x plus m y plus n equals 0 text end text$ is a normal to the ellipse $text end text fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1 text end text$ is

While drawing the map of USA, Jassica represented the distance between two cities as 2cm there the actual distance is 100km. What is the scale of the map.

While drawing the map of USA, Jassica represented the distance between two cities as 2cm there the actual distance is 100km. What is the scale of the map.

Height of 5 students in a classroom are 125 cm,134 cm, 157 cm,110 cm,146 cm.
Find the range of height

Height of 5 students in a classroom are 125 cm,134 cm, 157 cm,110 cm,146 cm.
Find the range of height

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.