Question
Davin keeps a record in graph form of how far his car travels and the number of gallons of gasoline it uses. What is the number of gallons that Davin uses per 32 miles?

- 1 gallon
- 2 gallons
- 4 gallons
- 8 gallons

Davin keeps record of graph about number of gallons of gasoline used while he was traveling. Here we have to find out the number of gallons in per 32 miles. To find that we have given graph. First find the how much miles its takes for 1 gallon and then multiply it to 32 . This help you to find the solutions.
The correct answer is: 1 gallon
Here we have to find out the total gallons of gasoline used per 32 miles.
Firstly , we have given graph, x-axis is gallons of gasoline and y-axis is miles.
According to graph, it has 3 point ,
Lets take points be a,b,c
We can easily tell the coordinate of b is (2,64) , which says that
The number of gallon used is 2 (it is x-axis coordinate) and miles travels is 64 ,
So here , for 64 miles its takes 2 gallons of gasoline,
To find 1 gallon , we have:
2 gallons = 64 miles
For 1 gallon we have to divide both side by 2 , we have
2/2 gallons = 64 /2 miles
1 gallons = 32 miles
Therefore , at per 32 miles car used 1 gallon of gasoline.
The correct answer is 1 gallon (option (a)).

To find the solution we have focus on the given coordinate on the graph. It will help you to find the x and y coordinate by that you can easily find the solution. And also find for one thing first and then by that you can easily find given thing. Apply the same concept in similar questions.
Related Questions to study
How many increasing and decreasing intervals are there in this graph?

It very easy to find the increasing and decreasing interval in graph you just have to focus on the graph where its going upward or downward or you can also find increasing and decreasing by finding the slope of the line. If the slope is positive then line is increasing otherwise slope is negative then line is decreasing.
How many increasing and decreasing intervals are there in this graph?

It very easy to find the increasing and decreasing interval in graph you just have to focus on the graph where its going upward or downward or you can also find increasing and decreasing by finding the slope of the line. If the slope is positive then line is increasing otherwise slope is negative then line is decreasing.
Look at the graph below and identify whether the function at interval 1 is increasing, decreasing or constant.

You can apply can process throughout any question related to increasing, decreasing and constant interval where you can find out easily by looking the graph or slope of line.
Look at the graph below and identify whether the function at interval 1 is increasing, decreasing or constant.

You can apply can process throughout any question related to increasing, decreasing and constant interval where you can find out easily by looking the graph or slope of line.
Which statement below accurately represents the graph?

In this question, We have to find the dollar earned in hour and which statement is true. Just read the graph carefully find x and y coordinate for same point. Apply same concept in similar questions.
Which statement below accurately represents the graph?

In this question, We have to find the dollar earned in hour and which statement is true. Just read the graph carefully find x and y coordinate for same point. Apply same concept in similar questions.
Identify the intervals in which the function is increasing.

For finding the increasing functions in interval you must consider the given interval will be going upward from left to right and you can see find the slope of interval if its positive then its increasing.
Identify the intervals in which the function is increasing.

For finding the increasing functions in interval you must consider the given interval will be going upward from left to right and you can see find the slope of interval if its positive then its increasing.
Identify the statement that best describes the increasing and decreasing of the graph.

It very easy to find the increasing and decreasing interval in graph you just have to focus on the graph where its going upward or downward or you can also find increasing and decreasing by finding the slope of the line. If the slope is positive then line is increasing otherwise slope is negative then line is decreasing.
Identify the statement that best describes the increasing and decreasing of the graph.

It very easy to find the increasing and decreasing interval in graph you just have to focus on the graph where its going upward or downward or you can also find increasing and decreasing by finding the slope of the line. If the slope is positive then line is increasing otherwise slope is negative then line is decreasing.
Which statement matches the graph?

In this question, we have to find the Taylor writing speed per minutes. Just read the graph carefully find x and y coordinate for same point, And then find y at x=1 . Apply same concept in similar questions.
Which statement matches the graph?

In this question, we have to find the Taylor writing speed per minutes. Just read the graph carefully find x and y coordinate for same point, And then find y at x=1 . Apply same concept in similar questions.
Find the constant rate of change.

Find the constant rate of change.

Identify whether the function is increasing, decreasing or constant at the interval pointed in the graph.

Identify whether the function is increasing, decreasing or constant at the interval pointed in the graph.

The table represents a linear function. What is the constant rate of change?

The table represents a linear function. What is the constant rate of change?

What is the definition of function?
Let us consider a function that defined as then, the representation may exist as shown below.
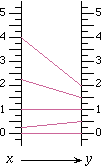
Hence, Every object x that belongs to the set of inputs has exactly one object y that belongs to the set of outputs.
*** Hence, the technical definition of the function is a relation from a set of i9nputs to set of possible outputs where each input is related to exactly one output.
What is the definition of function?
Let us consider a function that defined as then, the representation may exist as shown below.

Hence, Every object x that belongs to the set of inputs has exactly one object y that belongs to the set of outputs.
*** Hence, the technical definition of the function is a relation from a set of i9nputs to set of possible outputs where each input is related to exactly one output.



