Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

he equation $open parentheses cos invisible function application p minus 1 close parentheses x to the power of 2 end exponent plus open parentheses cos invisible function application p close parentheses x plus sin invisible function application p equals 0$ in the variable $x$ has real roots. Then $p$ can take any value in the interval

$3$
$\frac{8 \sqrt{3}}{3}$
$5$
$\frac{10 \sqrt{3}}{3}$

The correct answer is: $fraction numerator 10 square root of 3 over denominator 3 end fraction$

$375 blank$ In triangle $A B C comma blank angle A B C equals 120 degree comma blank A B equals 3 blank$ and $blank B C equals 4.$ If perpendicular constructed to the side $A B blank$ at $blank A$ and to the side $B C blank$ at $blank C$ meets at $D$ , then $blank C D$ is equal to
Note that $increment P C D$ is right angle as shown in the figure
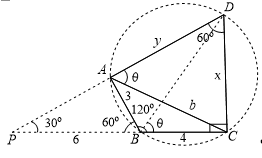
Now $blank tan invisible function application 30 degree equals fraction numerator x over denominator 10 end fraction$

$increment P A B blank$ is $blank 30 degree minus 60 degree minus 90 degree blank$ triangle, hence in $increment P A B comma blank P B equals fraction numerator 3 over denominator sin invisible function application 30 degree end fraction equals 6$
Therefore, in $blank increment P C D comma blank x equals 10 tan invisible function application 30 degree equals 10 divided by square root of 3 equals open parentheses 10 square root of 3 close parentheses divided by 3$
$open parentheses cos invisible function application p minus 1 close parentheses x to the power of 2 end exponent plus open parentheses cos invisible function application p close parentheses x plus sin invisible function application p equals 0$
For this equation to have real roots $D greater or equal than 0$
$rightwards double arrow cos to the power of 2 end exponent invisible function application p minus 4 sin invisible function application p blank open parentheses cos invisible function application p minus 1 close parentheses greater or equal than 0$
$rightwards double arrow cos to the power of 2 end exponent invisible function application p minus 4 sin invisible function application p cos invisible function application p plus 4 sin to the power of 2 end exponent invisible function application p plus 4 sin invisible function application p minus 4 sin to the power of 2 end exponent invisible function application p greater or equal than 0$
$rightwards double arrow open parentheses cos invisible function application p minus 2 sin invisible function application p close parentheses to the power of 2 end exponent plus 4 sin invisible function application p blank open parentheses 1 minus sin invisible function application p close parentheses greater or equal than 0$
For every real value of $p$ , we have
$open parentheses cos invisible function application p minus 2 sin invisible function application p close parentheses to the power of 2 end exponent greater or equal than 0$ and $sin invisible function application p left parenthesis 1 minus sin invisible function application p right parenthesis greater or equal than 0$
$therefore D greater or equal than 0 comma blank for all sin invisible function application p element of open parentheses 0 comma blank pi close parentheses$

Related Questions to study

he value of expression $square root of 3 c o s e c blank 20 degree minus sec invisible function application 20 degree$ is equal to

he value of expression $square root of 3 c o s e c blank 20 degree minus sec invisible function application 20 degree$ is equal to

$f cos invisible function application x equals fraction numerator 2 cos invisible function application y minus 1 over denominator 2 minus cos invisible function application y end fraction comma blank w h e r e blank x comma blank y element of open parentheses 0 comma blank pi close parentheses comma blank t h e n tan invisible function application fraction numerator x over denominator 2 end fraction cot invisible function application fraction numerator y over denominator 2 end fraction blank i s blank e q u a l blank t o$

$f cos invisible function application x equals fraction numerator 2 cos invisible function application y minus 1 over denominator 2 minus cos invisible function application y end fraction comma blank w h e r e blank x comma blank y element of open parentheses 0 comma blank pi close parentheses comma blank t h e n tan invisible function application fraction numerator x over denominator 2 end fraction cot invisible function application fraction numerator y over denominator 2 end fraction blank i s blank e q u a l blank t o$

he value of $cos invisible function application fraction numerator pi over denominator 7 end fraction plus cos invisible function application fraction numerator 2 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 3 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 4 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 5 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 6 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 7 pi over denominator 7 end fraction$ is

he value of $cos invisible function application fraction numerator pi over denominator 7 end fraction plus cos invisible function application fraction numerator 2 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 3 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 4 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 5 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 6 pi over denominator 7 end fraction plus cos invisible function application fraction numerator 7 pi over denominator 7 end fraction$ is

parallel

f $alpha plus beta equals pi divided by 2$ and $beta plus gamma equals alpha comma$ then $tan invisible function application alpha blank e q u a l s$

f $alpha plus beta equals pi divided by 2$ and $beta plus gamma equals alpha comma$ then $tan invisible function application alpha blank e q u a l s$

he smallest $plus v e blank x$ satisfying the equation $log subscript cos invisible function application x end subscript invisible function application sin invisible function application x plus log subscript sin invisible function application x end subscript invisible function application cos invisible function application x equals 2$ is

he smallest $plus v e blank x$ satisfying the equation $log subscript cos invisible function application x end subscript invisible function application sin invisible function application x plus log subscript sin invisible function application x end subscript invisible function application cos invisible function application x equals 2$ is

f $log subscript 4 end subscript invisible function application 5 equals a blank a n d log subscript 5 end subscript invisible function application 6 equals b comma$ then $log subscript 3 end subscript invisible function application 2$ is equal to

f $log subscript 4 end subscript invisible function application 5 equals a blank a n d log subscript 5 end subscript invisible function application 6 equals b comma$ then $log subscript 3 end subscript invisible function application 2$ is equal to

parallel

f in $increment A B C comma blank 8 R to the power of 2 end exponent equals a to the power of 2 end exponent plus b to the power of 2 end exponent plus c to the power of 2 end exponent comma$ then the triangle $A B C$ is

f in $increment A B C comma blank 8 R to the power of 2 end exponent equals a to the power of 2 end exponent plus b to the power of 2 end exponent plus c to the power of 2 end exponent comma$ then the triangle $A B C$ is

The total number of solutions of $open vertical bar cot invisible function application x close vertical bar equals cot invisible function application x plus fraction numerator 1 over denominator sin invisible function application x end fraction comma blank x element of open square brackets 0 comma blank 3 pi close square brackets$ is equal to

The total number of solutions of $open vertical bar cot invisible function application x close vertical bar equals cot invisible function application x plus fraction numerator 1 over denominator sin invisible function application x end fraction comma blank x element of open square brackets 0 comma blank 3 pi close square brackets$ is equal to

If the inequality $sin to the power of 2 end exponent invisible function application x plus a cos invisible function application x plus a to the power of 2 end exponent greater than 1 plus cos invisible function application x$ holds for any $x element of R comma$ then the largest negative integral value of $a$ is

If the inequality $sin to the power of 2 end exponent invisible function application x plus a cos invisible function application x plus a to the power of 2 end exponent greater than 1 plus cos invisible function application x$ holds for any $x element of R comma$ then the largest negative integral value of $a$ is

parallel

$fraction numerator sin invisible function application 3 theta plus sin invisible function application 5 theta plus sin invisible function application 7 theta plus sin invisible function application 9 theta over denominator cos invisible function application 3 theta plus cos invisible function application 5 theta plus cos invisible function application 7 theta plus cos invisible function application 9 theta end fraction blank i s blank e q u a l blank t o$

$fraction numerator sin invisible function application 3 theta plus sin invisible function application 5 theta plus sin invisible function application 7 theta plus sin invisible function application 9 theta over denominator cos invisible function application 3 theta plus cos invisible function application 5 theta plus cos invisible function application 7 theta plus cos invisible function application 9 theta end fraction blank i s blank e q u a l blank t o$

If $a to the power of 4 end exponent blank. b to the power of 5 end exponent equals 1 comma$ then the value of $log subscript a end subscript invisible function application open parentheses a to the power of 5 end exponent b to the power of 4 end exponent close parentheses$ equals

If $a to the power of 4 end exponent blank. b to the power of 5 end exponent equals 1 comma$ then the value of $log subscript a end subscript invisible function application open parentheses a to the power of 5 end exponent b to the power of 4 end exponent close parentheses$ equals

If $open parentheses x plus 1 close parentheses to the power of log subscript 10 end subscript invisible function application open parentheses x plus 1 close parentheses end exponent equals 100 open parentheses x plus 1 close parentheses comma$ then

If $open parentheses x plus 1 close parentheses to the power of log subscript 10 end subscript invisible function application open parentheses x plus 1 close parentheses end exponent equals 100 open parentheses x plus 1 close parentheses comma$ then

parallel

The sum of all the solution of $cot invisible function application theta equals sin invisible function application 2 theta comma blank open parentheses theta not equal to n pi comma n blank i n t e g e r close parentheses comma blank 0 less or equal than theta less or equal than pi blank$ is

The sum of all the solution of $cot invisible function application theta equals sin invisible function application 2 theta comma blank open parentheses theta not equal to n pi comma n blank i n t e g e r close parentheses comma blank 0 less or equal than theta less or equal than pi blank$ is

The number of solutions of the equation $sin to the power of 3 end exponent invisible function application x cos invisible function application x plus sin to the power of 2 end exponent invisible function application x cos to the power of 2 end exponent invisible function application x plus sin invisible function application x cos to the power of 3 end exponent invisible function application x equals 1 comma blank$ in the interval $open square brackets 0 comma blank 2 pi close square brackets comma blank$ is

The number of solutions of the equation $sin to the power of 3 end exponent invisible function application x cos invisible function application x plus sin to the power of 2 end exponent invisible function application x cos to the power of 2 end exponent invisible function application x plus sin invisible function application x cos to the power of 3 end exponent invisible function application x equals 1 comma blank$ in the interval $open square brackets 0 comma blank 2 pi close square brackets comma blank$ is

If $a comma blank b blank$ and $blank c$ are the sides of a triangle, then the minimum value of $fraction numerator 2 a over denominator b plus c minus a end fraction plus fraction numerator 2 b over denominator c plus a minus b end fraction plus fraction numerator 2 c over denominator a plus b minus c end fraction$ is

If $a comma blank b blank$ and $blank c$ are the sides of a triangle, then the minimum value of $fraction numerator 2 a over denominator b plus c minus a end fraction plus fraction numerator 2 b over denominator c plus a minus b end fraction plus fraction numerator 2 c over denominator a plus b minus c end fraction$ is

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.