Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Maths-

General

Easy

Question

If a curve $y equals 0 square root of x plus b x$ passes through the point $left parenthesis 1 comma blank 2 right parenthesis$ and the area bounded by the curve, Iine $x equals 4$ and $x$ ‐axis is 8 $s q$ units, then

$0 = 3,$ $b = - 1$
$0 = 3,$ $b = 1$
$0 = - 3,$ $b = 1$
$0 = - 3,$ $b = - 1$

The correct answer is: $0 equals 3 comma$ $b equals negative 1$

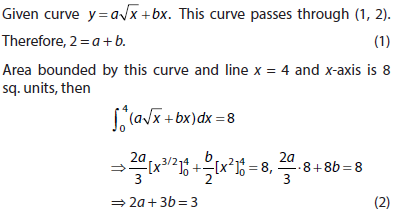
From equations (1) and (2), we get a = 3, b = -1.

Related Questions to study

The point of the contact of the tangent to the parabola $y to the power of 2 end exponent equals 4 a x$ , which makes an angle of 60° with x-axis, is

The point of the contact of the tangent to the parabola $y to the power of 2 end exponent equals 4 a x$ , which makes an angle of 60° with x-axis, is

The equation of the directrix of the parabola $x to the power of 2 end exponent plus 8 y minus 2 x equals 7$ is

The equation of the directrix of the parabola $x to the power of 2 end exponent plus 8 y minus 2 x equals 7$ is

The area enclosed by the parabolas $y equals x to the power of 2 end exponent minus 1$ and $y equals 1 minus x to the power of 2 end exponent$ is

The area enclosed by the parabolas $y equals x to the power of 2 end exponent minus 1$ and $y equals 1 minus x to the power of 2 end exponent$ is

parallel

The area between the curve $y to the power of 2 end exponent equals 4 o x comma$ $x$ -axis and the ordinates $x equals 0$ and $x equals o$ is

The area between the curve $y to the power of 2 end exponent equals 4 o x comma$ $x$ -axis and the ordinates $x equals 0$ and $x equals o$ is

The area of the region bounded by $y equals vertical line x minus 1 vertical line$ and $y equals 1$ is

The area of the region bounded by $y equals vertical line x minus 1 vertical line$ and $y equals 1$ is

The area of the plane region bounded by the curves $x plus 2 y to the power of 2 end exponent equals 0$ and $x plus 3 y to the power of 2 end exponent equals 1$ is equal to

The area of the plane region bounded by the curves $x plus 2 y to the power of 2 end exponent equals 0$ and $x plus 3 y to the power of 2 end exponent equals 1$ is equal to

parallel

The area bounded by the axes of reference and normal to $y equals I o g subscript e end subscript x$ at the point $left parenthesis 1 comma blank 0 right parenthesis$ is

The area bounded by the axes of reference and normal to $y equals I o g subscript e end subscript x$ at the point $left parenthesis 1 comma blank 0 right parenthesis$ is

The area bounded by the curve $y to the power of 2 end exponent equals 9 x$ and the line $x equals 1 comma x equals 4$ and $y equals 0$ in the first quadrant is

The area bounded by the curve $y to the power of 2 end exponent equals 9 x$ and the line $x equals 1 comma x equals 4$ and $y equals 0$ in the first quadrant is

The focus of the parabola $left parenthesis y minus 2 right parenthesis to the power of 2 end exponent equals 20 left parenthesis x plus 3 right parenthesis text is end text$

The focus of the parabola $left parenthesis y minus 2 right parenthesis to the power of 2 end exponent equals 20 left parenthesis x plus 3 right parenthesis text is end text$

parallel

The equation of the locus of a point which moves so as to be at equal distances from the point (a, 0) and the y-axis is

The equation of the locus of a point which moves so as to be at equal distances from the point (a, 0) and the y-axis is

$text The curve end text 16 x to the power of 2 end exponent plus 8 x y plus y to the power of 2 end exponent minus 74 x minus 78 y plus 212 equals 0 text represents end text$

$text The curve end text 16 x to the power of 2 end exponent plus 8 x y plus y to the power of 2 end exponent minus 74 x minus 78 y plus 212 equals 0 text represents end text$

The axis of the parabola $x to the power of 2 end exponent minus 4 x minus 3 y plus 10 equals 0 text is end text$

The axis of the parabola $x to the power of 2 end exponent minus 4 x minus 3 y plus 10 equals 0 text is end text$

parallel

Focus and directrix of the parabola $x to the power of 2 end exponent equals negative 8 a y text are end text$

Focus and directrix of the parabola $x to the power of 2 end exponent equals negative 8 a y text are end text$

If the vertex of a parabola be at origin and directrix be x + = 5 0, then its latus rectum is

If the vertex of a parabola be at origin and directrix be x + = 5 0, then its latus rectum is

10th-Grade-Math---USA

125, 80, 140, 135, 126, 140, 350, 75
Maximum value of given data _______________

125, 80, 140, 135, 126, 140, 350, 75
Maximum value of given data _______________

10th-Grade-Math---USAGeneral

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.