Question
The equation of normal on point (2,4) to the parabola y2 = 8x is-
- x + y = 6
- x – y + 2 = 0
- x + y = 2
- None of these

find out the slope of normal and use point and slope form to find the equation of normal.
The correct answer is: x + y = 6
x+y=6
Slope of tangent : dy/dx = 4/y
Slope of normal = -y/4
Equation of normal : y-4=-1(x-2)
y-4 = 2-x
x+y=6
we can also use equation of normal in slope form: y = mx – 2am – am3
Related Questions to study
Area of triangle formed by the tangents at three points t1, t2 and t3 of the parabola y2 = 4ax is-
area under a triangle is given by the determinant of the vertex points of the triangle.
Area of triangle formed by the tangents at three points t1, t2 and t3 of the parabola y2 = 4ax is-
area under a triangle is given by the determinant of the vertex points of the triangle.
The equation of the common tangents to the parabolas y2 = 4x and x2 = 32y is-
the equation of tangent to the parabola y2= 4ax is y = mx + a/m
The equation of the common tangents to the parabolas y2 = 4x and x2 = 32y is-
the equation of tangent to the parabola y2= 4ax is y = mx + a/m
The equation of tangent to the parabola x2 = y at one extremity of latus rectum in the first quadrant is
equation of tangent : T=0 of
X2= 4ay is given by
xx1=(y+y1)/2
The equation of tangent to the parabola x2 = y at one extremity of latus rectum in the first quadrant is
equation of tangent : T=0 of
X2= 4ay is given by
xx1=(y+y1)/2
The point of contact of the line 2x – y + 2 = 0 with the parabola y2 = 16 x is-
for a line to be a tangent of a parabola, the value of a/m should be equal to the value of c.
The point of contact of the line 2x – y + 2 = 0 with the parabola y2 = 16 x is-
for a line to be a tangent of a parabola, the value of a/m should be equal to the value of c.
The point on the curve y2 = x the tangent at which makes an angle of 45º with x-axis will be given by
the point of contact of a tangent with the curve is given by (x,y) =(a/m2, 2a/m). this is obtained by solving the equation of tangent with the equation of curve.
The point on the curve y2 = x the tangent at which makes an angle of 45º with x-axis will be given by
the point of contact of a tangent with the curve is given by (x,y) =(a/m2, 2a/m). this is obtained by solving the equation of tangent with the equation of curve.
The equation of the tangent to the parabola y = 2 + 4x –4x2 with slope –4 is
equation of a straight line : y-y1=m(x-x1)
m is given, calculate x1 and y1 by differentiating the equation of parabola and equating it with the slope.
The equation of the tangent to the parabola y = 2 + 4x –4x2 with slope –4 is
equation of a straight line : y-y1=m(x-x1)
m is given, calculate x1 and y1 by differentiating the equation of parabola and equating it with the slope.
The equation of the tangent at vertex to the parabola 4y2 + 6x = 8y + 7 is
if the slope of a line is infinite, then it is parallel to the y axis and the equation becomes x=a, where x is the x intercept.
Slope of the tangent : dy/dx
The equation of the tangent at vertex to the parabola 4y2 + 6x = 8y + 7 is
if the slope of a line is infinite, then it is parallel to the y axis and the equation becomes x=a, where x is the x intercept.
Slope of the tangent : dy/dx
The point where the line x + y = 1 touches the parabola y = x– x2 , is-
the point of intersection of two curves can be found out by solving the equations of the two curves,
The point where the line x + y = 1 touches the parabola y = x– x2 , is-
the point of intersection of two curves can be found out by solving the equations of the two curves,
The equation of the tangent to the parabola y2 = 4x at the point (1, 2) is-
Slope of tangent = dy/dx
Equation of line: y-y1 = m(x-x1)
The equation of the tangent to the parabola y2 = 4x at the point (1, 2) is-
Slope of tangent = dy/dx
Equation of line: y-y1 = m(x-x1)
If a tangent to the parabola 4y2 = x makes an angle of 60º with the x- axis, then its point of contact is-
point of contact = (a/m2, 2a/m)
slope = tan ( angle made with the x axis)
this gives us the value of m
y^2 = x/4 = 4(1/16)x
a = 1/16
If a tangent to the parabola 4y2 = x makes an angle of 60º with the x- axis, then its point of contact is-
point of contact = (a/m2, 2a/m)
slope = tan ( angle made with the x axis)
this gives us the value of m
y^2 = x/4 = 4(1/16)x
a = 1/16
At which point the line x = my +  touches the parabola x2 =4ay
touches the parabola x2 =4ay
the point of contact is the point of intersection between the 2 curves, the parabola and the line. this can be obtained by solving the two equations.
At which point the line x = my +  touches the parabola x2 =4ay
touches the parabola x2 =4ay
the point of contact is the point of intersection between the 2 curves, the parabola and the line. this can be obtained by solving the two equations.
For what value of k, the line 2y – x + k = 0 touches the parabola x2 + 4y = 0-
when a quadratic equation has 2 equal roots, the D value is 0 . D= b^2 - 4ac.=0
this gives us the possible value(s) of k
For what value of k, the line 2y – x + k = 0 touches the parabola x2 + 4y = 0-
when a quadratic equation has 2 equal roots, the D value is 0 . D= b^2 - 4ac.=0
this gives us the possible value(s) of k
An element, X has the following isotopic composition, 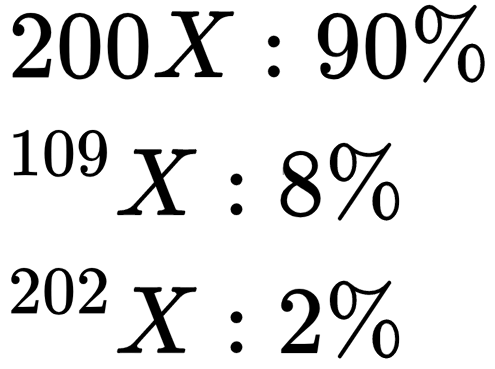 the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
An element, X has the following isotopic composition, 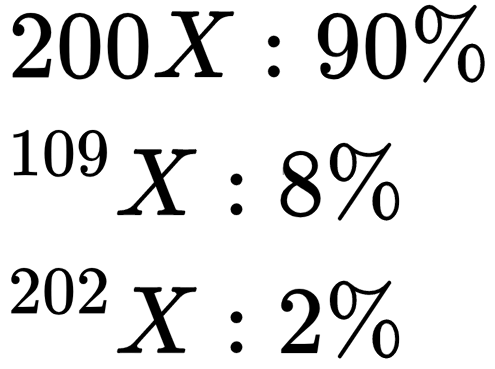 the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
the weighted average atomic mass of the naturally- occurring element 'X' is closest to :
The line  x + my + n = 0 will touch the parabola y2 = 4ax, if
x + my + n = 0 will touch the parabola y2 = 4ax, if
a quadratic equation has equal roots if the D value is zero. this is the condition of the line touching the curve.
The line  x + my + n = 0 will touch the parabola y2 = 4ax, if
x + my + n = 0 will touch the parabola y2 = 4ax, if
a quadratic equation has equal roots if the D value is zero. this is the condition of the line touching the curve.
The straight line 2x + y –1= 0 meets the parabola y2 = 4x in
when D> 0, two real and distinct roots
when D=0, real and equal roots
when D<0 imaginary roots.
The straight line 2x + y –1= 0 meets the parabola y2 = 4x in
when D> 0, two real and distinct roots
when D=0, real and equal roots
when D<0 imaginary roots.



