Have a query? Ask a Tutor!!

Access to best educators and exclusive paper discussions

Offsite Campus Turito Championship

Can’t find what you’re looking for?

Our tutors are from top schools around the world, and they are waiting for you 24/7, anytime, anywhere.

Homework- One to One Solutions
Understand concepts to solve better
Get your doubts solved instantly

Physics-

General

Easy

Question

At a certain place a magnet makes 30 oscillations per minute. At another place where the magnetic field is double, its time period will be

4 sec
2 sec
$\frac{1}{2} s e c$
$\sqrt{2} s e c$

The correct answer is: $square root of 2 s e c$

$T equals 2 pi square root of fraction numerator I over denominator M B subscript H end subscript end fraction end root semicolon therefore fraction numerator T subscript 1 end subscript over denominator T subscript 2 end subscript end fraction equals square root of fraction numerator left parenthesis B subscript H end subscript right parenthesis subscript 2 end subscript over denominator left parenthesis B subscript H end subscript right parenthesis subscript 1 end subscript end fraction end root rightwards double arrow T subscript 2 end subscript equals T subscript 1 end subscript square root of fraction numerator left parenthesis B subscript H end subscript right parenthesis subscript 1 end subscript over denominator left parenthesis B subscript H end subscript right parenthesis subscript 2 end subscript end fraction end root$
Here n₁=30 oscillation /min $equals fraction numerator 1 over denominator 2 end fraction$ oscillation/sec
$therefore fraction numerator mu over denominator 4 pi end fraction. fraction numerator m to the power of 2 end exponent over denominator r to the power of 2 end exponent end fraction equals 50 g m minus w t$
$therefore T subscript 2 end subscript equals 2 square root of fraction numerator B subscript H end subscript over denominator 2 B subscript H end subscript end fraction end root equals 2 cross times fraction numerator 1 over denominator square root of 2 end fraction equals square root of 2 s e c$

Related Questions to study

At which place, earth's magnetism become horizontal

At which place, earth's magnetism become horizontal

Physics-General

At a certain place the horizontal component of the earth’s magnetic field is B₀ and the angle of dip is 45^o. The total intensity of the field at that place will be

At a certain place the horizontal component of the earth’s magnetic field is B₀ and the angle of dip is 45^o. The total intensity of the field at that place will be

Physics-General

At a certain place, the horizontal component $B subscript 0 end subscript$ and the vertical component $V subscript 0 end subscript$ of the earth's magnetic field are equal in magnitude. The total intensity at the place will be

At a certain place, the horizontal component $B subscript 0 end subscript$ and the vertical component $V subscript 0 end subscript$ of the earth's magnetic field are equal in magnitude. The total intensity at the place will be

Physics-General

parallel

Lines which represent places of constant angle of dip are called

Lines which represent places of constant angle of dip are called

Physics-General

At a place, the horizontal and vertical intensities of earth's magnetic field is 0.30 Gauss and 0.173 Gauss respectively. The angle of dip at this place is

At a place, the horizontal and vertical intensities of earth's magnetic field is 0.30 Gauss and 0.173 Gauss respectively. The angle of dip at this place is

Physics-General

The angle of dip is the angle

The angle of dip is the angle

Physics-General

parallel

If the normal at the points P_i (x_i, y_i), i = 1 to 4 on the hyperbola xy = c² are concurrent at the point Q(h, k), then $fraction numerator open parentheses x subscript 1 end subscript plus x subscript 2 end subscript plus x subscript 3 end subscript plus x subscript 4 end subscript close parentheses open parentheses y subscript 1 end subscript plus y subscript 2 end subscript plus y subscript 3 end subscript plus y subscript 4 end subscript close parentheses over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction$ is equal to

If the normal at the points P_i (x_i, y_i), i = 1 to 4 on the hyperbola xy = c² are concurrent at the point Q(h, k), then $fraction numerator open parentheses x subscript 1 end subscript plus x subscript 2 end subscript plus x subscript 3 end subscript plus x subscript 4 end subscript close parentheses open parentheses y subscript 1 end subscript plus y subscript 2 end subscript plus y subscript 3 end subscript plus y subscript 4 end subscript close parentheses over denominator x subscript 1 end subscript x subscript 2 end subscript x subscript 3 end subscript x subscript 4 end subscript end fraction$ is equal to

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

The most general form of the equation of a conic is given by $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ . Let x and y-axes be respectively tangent and normal to the conic given by equation ((a) at the origin. Then clearly c = 0. Also by putting y = 0, we get $a x to the power of 2 end exponent plus 2 g x$ = 0. Both roots of the equation are zero. Therefore g = 0.
Hence the most general form of the equation of such a conic is given by $blank a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 f y equals 0$ .
Let foci of the conic represented by the equation $blank a x to the power of 2 end exponent plus 2 left parenthesis a plus 2 right parenthesis x y plus a y to the power of 2 end exponent plus 2 f y equals 0$ , where $a less than negative 1$ and $f not equal to 0$ be $F subscript 1 end subscript left parenthesis 2 comma negative 3 right parenthesis blank$ and $blank F subscript 2 end subscript left parenthesis 8 comma negative 5 right parenthesis$ . Then the feet of perpendiculars from F₁ and F₂ upon x-axis lie on the curve

According to Huckel’s rule a compound is said to be aromatic if it contains

According to Huckel’s rule a compound is said to be aromatic if it contains

Chemistry-General

parallel

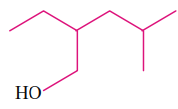structure is

structure is

Chemistry-General

Two volatile liquids A and B differ in their boiling points by 0 15 C The process which can be used to separate them is

Two volatile liquids A and B differ in their boiling points by 0 15 C The process which can be used to separate them is

Chemistry-General

Consider the ellipse whose equation is $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ For certain pair of diameters of the above ellipse, the product of their slopes is equal to $negative fraction numerator b to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction$
The equations of two diameters are $y equals x$ and $3 y equals negative 2 x$ satisfying the condition mentioned above. Then the eccentricity of the ellipse is

Consider the ellipse whose equation is $fraction numerator x to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction plus fraction numerator y to the power of 2 end exponent over denominator b to the power of 2 end exponent end fraction equals 1$ For certain pair of diameters of the above ellipse, the product of their slopes is equal to $negative fraction numerator b to the power of 2 end exponent over denominator a to the power of 2 end exponent end fraction$
The equations of two diameters are $y equals x$ and $3 y equals negative 2 x$ satisfying the condition mentioned above. Then the eccentricity of the ellipse is

parallel

The smallest possible value of S $equals a subscript 1 end subscript times a subscript 2 end subscript times a subscript 3 end subscript plus b subscript 1 end subscript times b subscript 2 end subscript times b subscript 3 end subscript plus c subscript 1 end subscript times c subscript 2 end subscript times c subscript 3 end subscript text end text$ where $text end text a subscript 1 end subscript comma a subscript 2 end subscript comma a subscript 3 end subscript comma b subscript 1 end subscript comma b subscript 2 end subscript comma b subscript 3 end subscript comma c subscript 1 end subscript comma c subscript 2 end subscript comma c subscript 3 end subscript$ is a permutation of the number 1, 2, 3, 4, 5, 6, 7, 8, and 9 is

The smallest possible value of S $equals a subscript 1 end subscript times a subscript 2 end subscript times a subscript 3 end subscript plus b subscript 1 end subscript times b subscript 2 end subscript times b subscript 3 end subscript plus c subscript 1 end subscript times c subscript 2 end subscript times c subscript 3 end subscript text end text$ where $text end text a subscript 1 end subscript comma a subscript 2 end subscript comma a subscript 3 end subscript comma b subscript 1 end subscript comma b subscript 2 end subscript comma b subscript 3 end subscript comma c subscript 1 end subscript comma c subscript 2 end subscript comma c subscript 3 end subscript$ is a permutation of the number 1, 2, 3, 4, 5, 6, 7, 8, and 9 is

Statement 1 : The second degree equation $4 x to the power of 2 end exponent plus 9 y to the power of 2 end exponent minus 24 x plus 36 y minus 72 equals 0$ represents an ellipse Because
Statement 2 : $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 g x plus 2 f y plus c equals 0$ represents an ellipse if $capital delta equals a b c plus 2 f g h minus a f to the power of 2 end exponent minus b g to the power of 2 end exponent minus c h to the power of 2 end exponent not equal to 0$ and $h to the power of 2 end exponent greater than a b$

Statement 1 : The second degree equation $4 x to the power of 2 end exponent plus 9 y to the power of 2 end exponent minus 24 x plus 36 y minus 72 equals 0$ represents an ellipse Because
Statement 2 : $a x to the power of 2 end exponent plus 2 h x y plus b y to the power of 2 end exponent plus 2 g x plus 2 f y plus c equals 0$ represents an ellipse if $capital delta equals a b c plus 2 f g h minus a f to the power of 2 end exponent minus b g to the power of 2 end exponent minus c h to the power of 2 end exponent not equal to 0$ and $h to the power of 2 end exponent greater than a b$

Statement-1: P is any point such that the chord of contact of tangents from P to the ellipse $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ touches $x to the power of 2 end exponent plus 4 y to the power of 2 end exponent equals 4$ The the tangents from P of $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ are at right angles and
Statement-2: The tangent from any point on the director circle of an ellipse are at right angles

Statement-1: P is any point such that the chord of contact of tangents from P to the ellipse $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ touches $x to the power of 2 end exponent plus 4 y to the power of 2 end exponent equals 4$ The the tangents from P of $x to the power of 2 end exponent plus 2 y to the power of 2 end exponent equals 6$ are at right angles and
Statement-2: The tangent from any point on the director circle of an ellipse are at right angles

parallel

card img

With Turito Academy.

card img

With Turito Foundation.

card img

Get an Expert Advice From Turito.

Turito Academy

card img

With Turito Academy.

Test Prep

card img

With Turito Foundation.