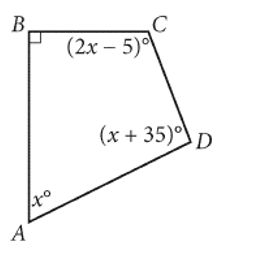
Question
A length of 8 furlongs is equivalent to how many meters? (Use 1 furlong = 201 meters.)
- 25
- 40
- 209
- 1,608
The correct answer is: 1,608
We multiply with the number of units.
Explanations:
Step 1 of 1:
Given, 1 furlong = 201 meters
Then, 8 furlongs = 8 × 201 = 1608 meters
Final Answer:
The equivalent length, in meters, is — 1608
Related Questions to study
If 2x + 4 = 100, what is the value of 6x + 12 ?
If 2x + 4 = 100, what is the value of 6x + 12 ?
It takes 6 hours to travel m miles. At this rate, how much time, in hours, will it take to travel 5 m miles?
It takes 6 hours to travel m miles. At this rate, how much time, in hours, will it take to travel 5 m miles?
 The given function
The given function  models the number of flour beetles in a certain area, where
models the number of flour beetles in a certain area, where  represents the number of days after June 1. Which of the following is the best interpretation of the number 1.11 in this context?
represents the number of days after June 1. Which of the following is the best interpretation of the number 1.11 in this context?
 The given function
The given function  models the number of flour beetles in a certain area, where
models the number of flour beetles in a certain area, where  represents the number of days after June 1. Which of the following is the best interpretation of the number 1.11 in this context?
represents the number of days after June 1. Which of the following is the best interpretation of the number 1.11 in this context?
8x - 4y = 7
3x + 6y = 12
If (x, y) is the solution to the given system of equations, what is the value of x ?
8x - 4y = 7
3x + 6y = 12
If (x, y) is the solution to the given system of equations, what is the value of x ?
Albedos of Various Earth Surfaces

An albedo is the amount of light reflected from a surface divided by the amount of light falling on the surface. The amount is typically measured in watts per square meter. The table shows the minimum and maximum albedos for different types of surfaces on Earth.
In a desert region, the amount of sunlight falling on a surface with an area of one square meter is 1,000 watts. Which of the following could be the amount of sunlight, in watts, reflected from this one-square-meter surface?
Albedos of Various Earth Surfaces

An albedo is the amount of light reflected from a surface divided by the amount of light falling on the surface. The amount is typically measured in watts per square meter. The table shows the minimum and maximum albedos for different types of surfaces on Earth.
In a desert region, the amount of sunlight falling on a surface with an area of one square meter is 1,000 watts. Which of the following could be the amount of sunlight, in watts, reflected from this one-square-meter surface?
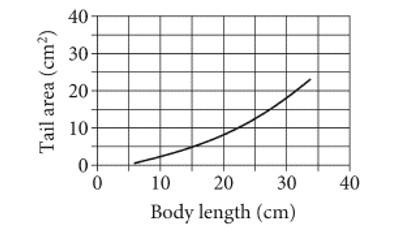
For a certain group of fish, the graph models the relationship between body length L, in centimeters (cm), and tail area A, in square centimeters  , where
, where  . Which equation represents the relationship between body length and tail area?
. Which equation represents the relationship between body length and tail area?
Solving quadratic equations using a graph is an effective method for locating estimated solutions or roots for quadratic equations or functions.
The real roots of a quadratic function might be zero, one (repeated), or two. Finding the origins involves solving a quadratic equation with the right-hand side equal to zero, such as ax² + bx + c = 0.
Points to consider to solve a quadratic equation using a graph :
• Rearrange the equation so that one side corresponds to the graphed function.
• Plot the function y= the other side of the equation.
• To find the solutions, draw vertical lines down to the x-axis from the intersection points.

For a certain group of fish, the graph models the relationship between body length L, in centimeters (cm), and tail area A, in square centimeters  , where
, where  . Which equation represents the relationship between body length and tail area?
. Which equation represents the relationship between body length and tail area?
Solving quadratic equations using a graph is an effective method for locating estimated solutions or roots for quadratic equations or functions.
The real roots of a quadratic function might be zero, one (repeated), or two. Finding the origins involves solving a quadratic equation with the right-hand side equal to zero, such as ax² + bx + c = 0.
Points to consider to solve a quadratic equation using a graph :
• Rearrange the equation so that one side corresponds to the graphed function.
• Plot the function y= the other side of the equation.
• To find the solutions, draw vertical lines down to the x-axis from the intersection points.
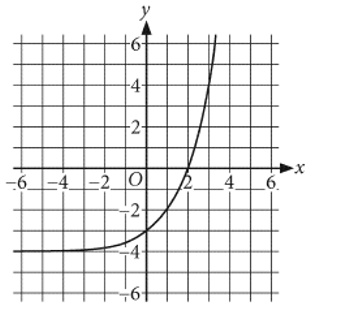
The graph of  is shown, where a is a constant. What is the value of a ?
is shown, where a is a constant. What is the value of a ?

The graph of  is shown, where a is a constant. What is the value of a ?
is shown, where a is a constant. What is the value of a ?
Which of the following is(are) an x - intercept of the graph of  in the xy - plane?
in the xy - plane?
I. (- 3,0)
II. (2, 0)
III. (0, 0)
Which of the following is(are) an x - intercept of the graph of  in the xy - plane?
in the xy - plane?
I. (- 3,0)
II. (2, 0)
III. (0, 0)
The function f is a linear function. The y - intercept of the graph of y = f(x) in the xy -plane is (0, - 12). What is the y-intercept of the graph of y = f(x) + 2 ?
The function f is a linear function. The y - intercept of the graph of y = f(x) in the xy -plane is (0, - 12). What is the y-intercept of the graph of y = f(x) + 2 ?
 The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
 The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
The given equation relates the variables c, x, and y, where c > 0, x > 0, and y > 0. Which equation correctly expresses y in terms of c and x ?
In the xy-plane, line l has a slope of 2. Line k is perpendicular to line l and contains the point (4, 2). Which of the following is an equation of line k ?
In the xy-plane, line l has a slope of 2. Line k is perpendicular to line l and contains the point (4, 2). Which of the following is an equation of line k ?
In right triangle ABC, the length of side  is 12 , the measure of
is 12 , the measure of  is
is  , and
, and  is a right angle. Which of the following can be determined using the information given?
is a right angle. Which of the following can be determined using the information given?
I) The measure of 
II) The length of side 
Any triangle that has one 90-degree angle is said to have a right angle. Right triangles are those with an angle of 90 degrees, or "right angles," hence those with this angle. First, determine the third angle's measurement. You already know that C = 90 degrees because it is a right angle, and you are also aware of the size of A or B. Since a triangle's internal degree measurement must always equal 180 degrees, the third angle's measurement can be determined by applying the following formula: 180 – (90 + A) = B. The formula can also be turned around so that 180 - (90 + B) = A.
As an illustration, if you know that A is 40 degrees, then B is 180 – (90 – 40). It is easy to work out that B = 50 degrees if you simplify this to B = 180 - 130. Triangles can be resolved using the Law of Sines. Knowing the length of one side and the measurement of one other angle in addition to the right angle will especially assist you in finding the hypotenuse of a right triangle. The Law of Sines asserts that for any triangle with sides a, b, and c and angles a, b, and c, a / sin A = b / sin B = c / sin C.
Any triangle can be resolved using the Law of Sines, but only a right triangle will have a hypotenuse.
In right triangle ABC, the length of side  is 12 , the measure of
is 12 , the measure of  is
is  , and
, and  is a right angle. Which of the following can be determined using the information given?
is a right angle. Which of the following can be determined using the information given?
I) The measure of 
II) The length of side 
Any triangle that has one 90-degree angle is said to have a right angle. Right triangles are those with an angle of 90 degrees, or "right angles," hence those with this angle. First, determine the third angle's measurement. You already know that C = 90 degrees because it is a right angle, and you are also aware of the size of A or B. Since a triangle's internal degree measurement must always equal 180 degrees, the third angle's measurement can be determined by applying the following formula: 180 – (90 + A) = B. The formula can also be turned around so that 180 - (90 + B) = A.
As an illustration, if you know that A is 40 degrees, then B is 180 – (90 – 40). It is easy to work out that B = 50 degrees if you simplify this to B = 180 - 130. Triangles can be resolved using the Law of Sines. Knowing the length of one side and the measurement of one other angle in addition to the right angle will especially assist you in finding the hypotenuse of a right triangle. The Law of Sines asserts that for any triangle with sides a, b, and c and angles a, b, and c, a / sin A = b / sin B = c / sin C.
Any triangle can be resolved using the Law of Sines, but only a right triangle will have a hypotenuse.