Question
Forces of magnitudes  and
and  act at a point parallel to the sides of an equilateral triangle taken in order. The resultant of these forces, is
act at a point parallel to the sides of an equilateral triangle taken in order. The resultant of these forces, is



- 3P

In this question, we have given a equilateral triangle and the force of magnitude is parallel with the sides of triangle. Which is P- Q, P, P + Q. We have to find the resultant force. Find the component of force for each magnitude.
The correct answer is: 
Here,

Þ  =
=  …..(i)
…..(i)

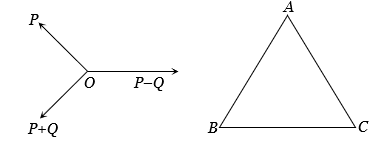
Þ 
 =
=  …..(ii)
…..(ii)
Squaring and adding (i) and (ii), we get


 .
.
Here we have to find the resultant force.
Now, we have 3 magnitudes of force,
a = P, b = P – Q, c = P + Q,
Now the component of force,
At A, θ= 60°
acos θ = P cos 60° =
asin θ = P sin 60° = 
At C, θ= 60°
c cos θ = P+Q cos 60° = 
c sin θ = P+Q sin 60° = 
No component for B because it is at x- axis.
So Resultant force is,
Fi = ( 
 + P – Q ) i^
+ P – Q ) i^
Fi = ( 
 - Q/2 + P – Q ) i^
- Q/2 + P – Q ) i^
Fi = (  ) i^
) i^
And
Fj = ( ) j^
) j^
Fj = (  ) j^
) j^
Fj = (  ) j^
) j^
Therefore,
|F| = 
|F| = 
|F| = 
|F| = 
|F| = 
Therefore, the resultant force is 
The correct answer is  .
.
Here we have to find the resultant force of the given magnitude. Firstly, find the component of the force which is Fsin θ and Fcos θ.
Related Questions to study
If two forces  and
and  make an angle
make an angle 
 with each other and their resultant makes an angle
with each other and their resultant makes an angle  with the bisector of the angle between the two forces, then is equal to
with the bisector of the angle between the two forces, then is equal to
If two forces  and
and  make an angle
make an angle 
 with each other and their resultant makes an angle
with each other and their resultant makes an angle  with the bisector of the angle between the two forces, then is equal to
with the bisector of the angle between the two forces, then is equal to
If the square of the resultant of two equal forces is equal to  times their product, then the angle between the forces is
times their product, then the angle between the forces is
If the square of the resultant of two equal forces is equal to  times their product, then the angle between the forces is
times their product, then the angle between the forces is
The maximum resultant of two forces is P and the minimum resultant is  , the two forces are at right angles, the resultant is
, the two forces are at right angles, the resultant is
The maximum resultant of two forces is P and the minimum resultant is  , the two forces are at right angles, the resultant is
, the two forces are at right angles, the resultant is
The resultant of two forces  and
and  is of magnitude P. If the force
is of magnitude P. If the force  is doubled,
is doubled,  remaining unaltered, the new resultant will be
remaining unaltered, the new resultant will be
The resultant of two forces  and
and  is of magnitude P. If the force
is of magnitude P. If the force  is doubled,
is doubled,  remaining unaltered, the new resultant will be
remaining unaltered, the new resultant will be
The resultant of two forces 3P and 2P is R, if the first force is doubled, the resultant is also doubled. The angle between the forces is
In this question, we have to make two equations of Resultant as per given instruction and solve the equations and find the angle. Remember the formula of Resultant is R =
The resultant of two forces 3P and 2P is R, if the first force is doubled, the resultant is also doubled. The angle between the forces is
In this question, we have to make two equations of Resultant as per given instruction and solve the equations and find the angle. Remember the formula of Resultant is R =
If the gradient of the tangent at any point (x, y) of a curve which passes through the point  is
is  then equation of the curve is
then equation of the curve is
If the gradient of the tangent at any point (x, y) of a curve which passes through the point  is
is  then equation of the curve is
then equation of the curve is
If  , then
, then  is
is
In this question, we have given ycosx + xcosy =π . Differentiate this equation with request to x and do separate second derivate and find the value of it.
If  , then
, then  is
is
In this question, we have given ycosx + xcosy =π . Differentiate this equation with request to x and do separate second derivate and find the value of it.
The solution of the differential equation  is equal to
is equal to
In this question, you have to find the solution of differential equation x4 + x3 y + cosec (xy) = 0. Use variable separable method to find the solution.
The solution of the differential equation  is equal to
is equal to
In this question, you have to find the solution of differential equation x4 + x3 y + cosec (xy) = 0. Use variable separable method to find the solution.





